Предмет: Алгебра,
автор: Xonda7777
Найти решение задачи Коши
Приложения:
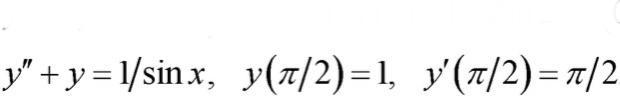
Ответы
Автор ответа:
1
Ответ:
Решаем ЛНДУ 2-го порядка с постоянными коэффициентами методом вариации произвольных постоянных ( методом Лагранжа ) .
1) Cначала решаем ЛОДУ 2-го порядка и находим его общее решение .
2) Ищем решение ЛНДУ 2-го порядка в виде
Чтобы найти функции решаем систему
,
.
Решаем систему методом Крамера .
Зная производные функций , восстанавливаем сами функции с помощью интегрирования .
Запишем общее решение заданного ЛНДУ 2-го порядка :
3) Найдём частное решение ЛНДУ 2-го порядка , соответствующее заданным начальным условиям .
Решение ищем в окрестности точки х = П/2, тогда sin х > 0 , |sinx|=sinx
Частное решение имеет вид:
Приложения:



Похожие вопросы
Предмет: Английский язык,
автор: angelinagoma153
Предмет: Химия,
автор: v6138281
Предмет: Химия,
автор: lll379887
Предмет: Физика,
автор: shakbanov2015
Предмет: Математика,
автор: stasyignatenko