Предмет: Алгебра,
автор: Xonda7777
Найти решение задачи Коши
Приложения:
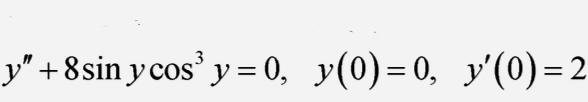
ВикаБач:
2 раза продифференцируй.; cosy=t;
Ответы
Автор ответа:
1
Обозначим . Тогда
, где точкой обозначена производная по
.
В наших переменных
Тогда,
Имеем . Поскольку
, то данное уравнение равносильно уравнению
В силу получим, что
.
Ответ. .
Похожие вопросы
Предмет: Информатика,
автор: lufi68549
Предмет: Химия,
автор: liza35112
Предмет: Русский язык,
автор: gofkenovaa
Предмет: Химия,
автор: TheAgentSquid
Предмет: Математика,
автор: vladislavm54