Question

Решить с рисунком, и правильным пошаговым оформлением !

Answer 1

Ответ:

Объяснение:

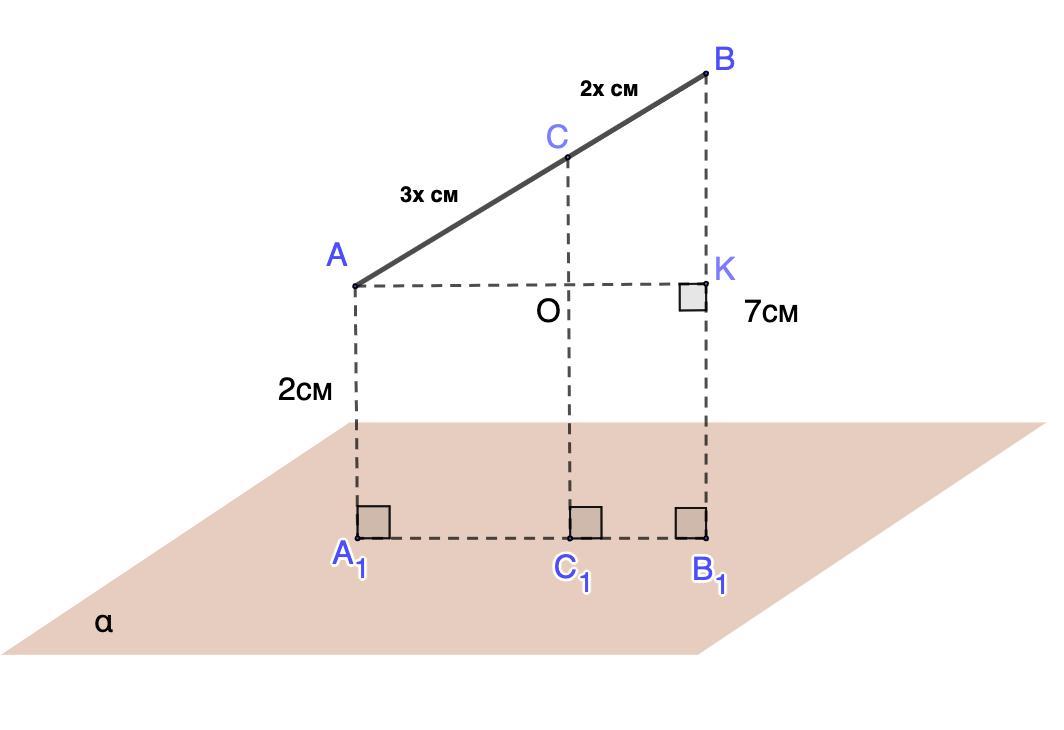
Дана плоскость α и не пересекающий её отрезок АВ. Кратчайшие расстояния от концов отрезка АВ до плоскости α AA₁ = 2 см и BB₁=7 см. Отрезок АВ разделили точкой С в отношении 3 : 2, считая от вершины А.

Найдите кратчайшее расстояние (см) от точки С до плоскости α.

Дано: плоскость α;

АВ ⊄ α;

AA₁ = 2 см и BB₁ = 7 см;

АС : СВ = 3 : 2

Найти: кратчайшее расстояние (см) от точки С до плоскости α.

Решение:

• Кратчайшее расстояние от точки до плоскости - длина перпендикуляра, опущенного из данной точки на данную плоскость.

⇒ АА₁ ⊥ α; ВВ₁ ⊥ α.

• Если две прямые перпендикулярны к плоскости, то они параллельны между собой.

⇒  АА₁ || ВВ₁

• Через две параллельные прямые можно провести плоскость, причем только одну.

• Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

⇒  А₁АВ ⊥ α.

А₁АВ ∩ α = А₁В₁

Проведем СС₁ ⊥ А₁В₁

• Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна другой плоскости.

⇒ СС₁ ⊥ α

СС₁ - искомый отрезок.

Проведем АК ⊥ ВВ₁.

АА₁КВ₁ - прямоугольник.

⇒ АА₁ = КВ₁ = 2 см, тогда КВ = 7 - 2 = 5 (см)

АА₁ОС₁ - прямоугольник.

⇒ ОС₁ = 2 см.

АС : СВ = 3 : 2

Пусть АС = 3х см, тогда СВ = 2х см, а АВ = 5х см.

Рассмотрим ΔАСО и ΔАВК- прямоугольные.

∠КАВ - общий.

⇒ ΔАСО ~ ΔАВК (по двум углам)

Запишем отношения сходственных сторон:

$\displaystyle \frac{AC}{AB}=\frac{CO}{BK} \\\\\frac{3x}{5x}=\frac{CO}{5} \;\;\;\Rightarrow \;\;\;CO=\frac{3x\cdot5}{5x} =3\;_{(CM)}$

CC₁ = 2 + 3 = 5 (см)

Кратчайшее расстояние (см) от точки С до плоскости α равно 5 см.