Question

Биссектриса острого угла прямоугольного треугольника делит противолежащий катет на отрезки длины 25 и 24. Найдите длину гипотенузы

Answer 1

Ответ:

175.

Пошаговое объяснение:

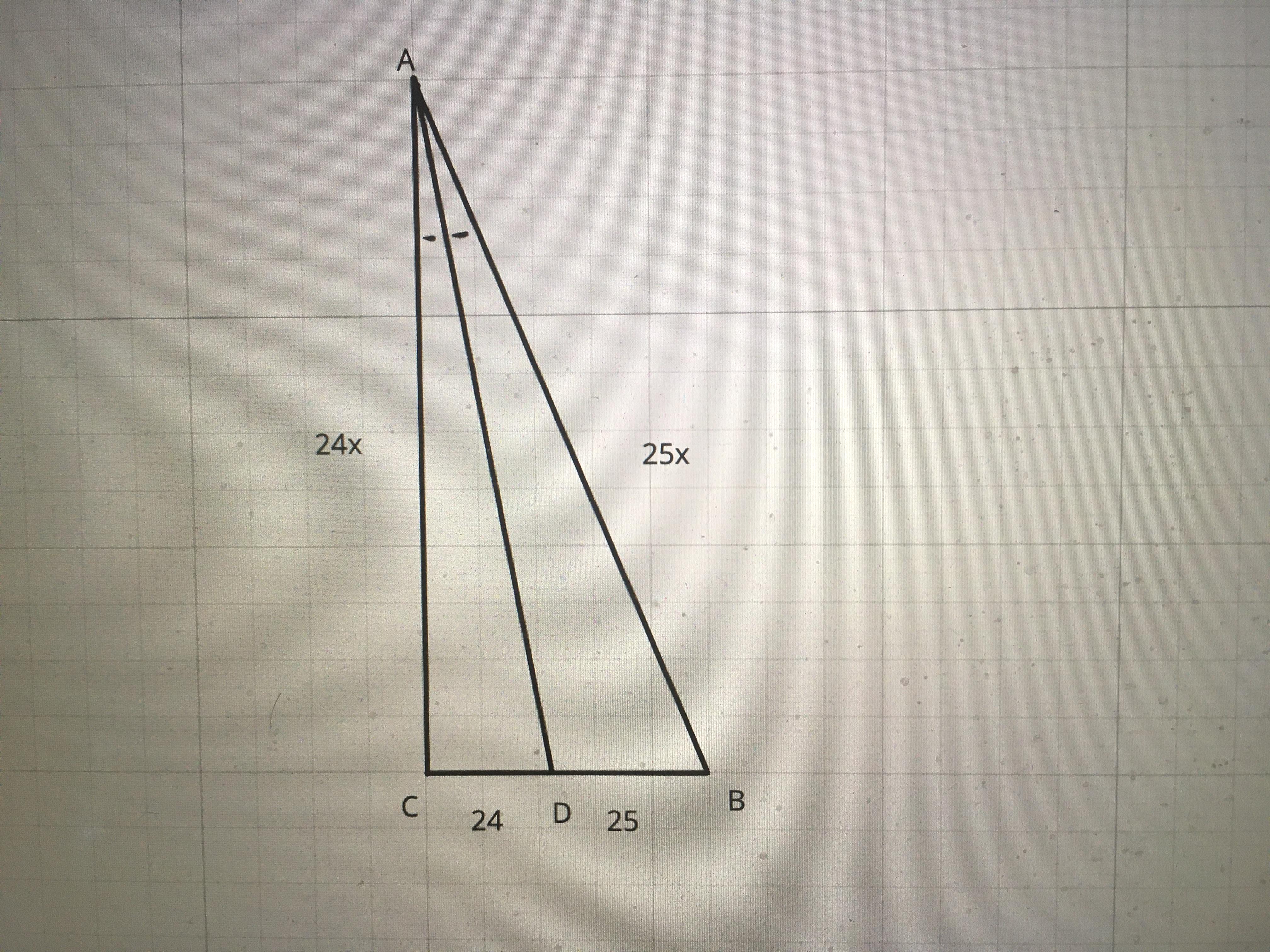
Дан прямоугольный треугольник ABC (угол C прямой); AD - биссектриса. По условию CD=24; DB=25⇒ CB=49. По известному свойству биссектрисы

                                           $\dfrac{AC}{AB}=\dfrac{CD}{DB},$

поэтому AC=24x, AB=25x.

По теореме Пифагора

   $AB^2-AC^2=CB^2;\ 25^2x^2-24^2x^2=49^2;\ (25-24)(25+24)x^2=49^2;$

            $49x^2=49^2;\ x^2=49;\ x=7\Rightarrow AB=25x=25\cdot 7=175.$

Замечание. Мы взяли CD=24, DB=25, а не наоборот, так как иначе у нас гипотенуза оказалась бы меньше катета.