Предмет: Алгебра,
автор: Dillety
решение с объяснннием
Приложения:
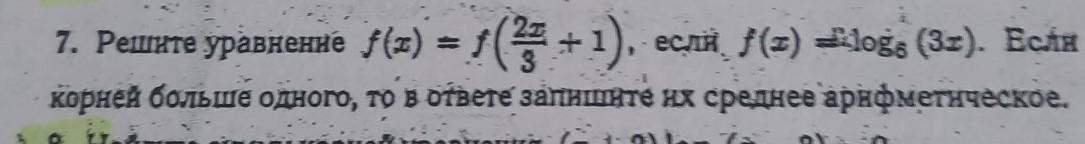
Alexandr130398:
x=3
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Объяснение:
Способ 1:
- это монотонно возрастающая функция, поэтому верно, что:
Обращаю внимание, что нам просто важно, чтобы функция возрастала / убывала на всей области определения, то есть Вам могли бы дать точно такую же задачу и сказать, что . Ответ все равно был бы
.
Вообще задача странная, так как не понятно, на проверку чего она дана. Предположу, что какой-то школьный преподаватель решил придумать задачу лето и предложу способ 2.
Способ 2:
Тогда получили уравнение:
ОДЗ:
Решение:
Найденный корень удовлетворяет ОДЗ, а значит - это корень исходного уравнения.
Задание выполнено!
Похожие вопросы
Предмет: Українська мова,
автор: dasha27272
Предмет: Биология,
автор: ergwj9erfgjngfjuniof
Предмет: Химия,
автор: nyubaraliyevaa
Предмет: Информатика,
автор: Iylialadkina
Предмет: Английский язык,
автор: anastasia25Petrenko