Предмет: Алгебра,
автор: Xonda7777
Найти общий интеграл дифференциального уравнения.
Приложения:
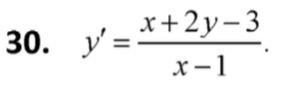
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Объяснение:
Замена: .
Замена: .
- особое решение
Отметим, что указанное нами выше особое решение входит в общее при .
Уравнение решено!
Xonda7777:
Спасибо вам огромное
Похожие вопросы
Предмет: Литература,
автор: wwxx88
Предмет: Английский язык,
автор: ivanvalik220
Предмет: Английский язык,
автор: alia20110508
Предмет: Геометрия,
автор: bakytgulkabdolla2