Question

Запиши всі трицифрові числа, у яких число десятків на 2 більше, а число сотень - удвічі більше ніж число одиниць.

Answer 1

Позначимо число одиниць як $x$. Тоді число десятків буде $(x+2)$, а число сотень повинно бути $2x$

Тепер ми можемо створити трицифрові числа за цими умовами. Ці числа матимуть вигляд "сотні + десятки + одиниці".

$2 \cdot x \cdot100 + (x + 2) \cdot 10 + x=211x+20$

Знайдемо значення "x", яке задовольняє цю нерівність:

$211x+20 < 999$

Тут максимальне значення для x = 4, оскільки при x = 5 ми отримаємо 1055, що вже перевищує трьохзначні числа.

Тепер ми можемо підставити значення x в рівняння і знайти числа, які задовольняють умовам:

x = 1: 211 * 1 + 20 = 231

x = 2: 211 * 2 + 20 = 442

x = 3: 211 * 3 + 20 = 653

x = 4: 211 * 4 + 20 = 864

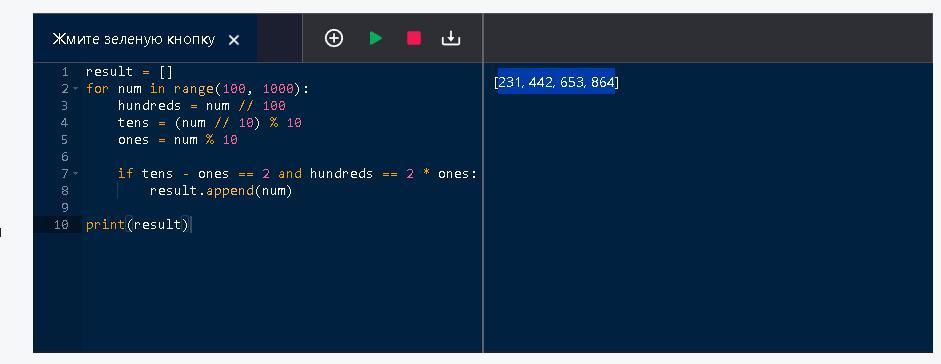
Отже, числа 231, 442, 653 і 864 відповідають умовам, які ви подали.

Для коректної перевірки виведемо результат за допомогою мови Python на фото.

Відповідь: 231, 442, 653, 864.