Предмет: Математика,
автор: misha200520
Найти частные производные первого порядка второго порядка проверить равенство Найти дифференциалы
Приложения:
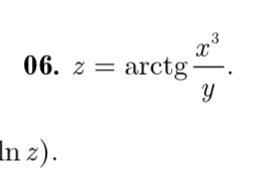

Ответы
Автор ответа:
1
Ответ:
Частные производные .
При нахождении производной функции по одной из переменных, вторая считается константой .
Проверим равенство смешанных производных .
Дифференциал 2 порядка равен
.
Приложения:


Похожие вопросы
Предмет: Математика,
автор: kamolaasadovna
Предмет: Математика,
автор: polidvurech
Предмет: География,
автор: denisstarovackij
Предмет: Биология,
автор: Ffaruth
Предмет: Химия,
автор: gbobrov945