Предмет: Алгебра,
автор: lajzamak
(2a/a-7 - 4a/a²-14a+49) : (a-9/a²-49 +28a/7-a) = 2a довести тотожність
Приложения:
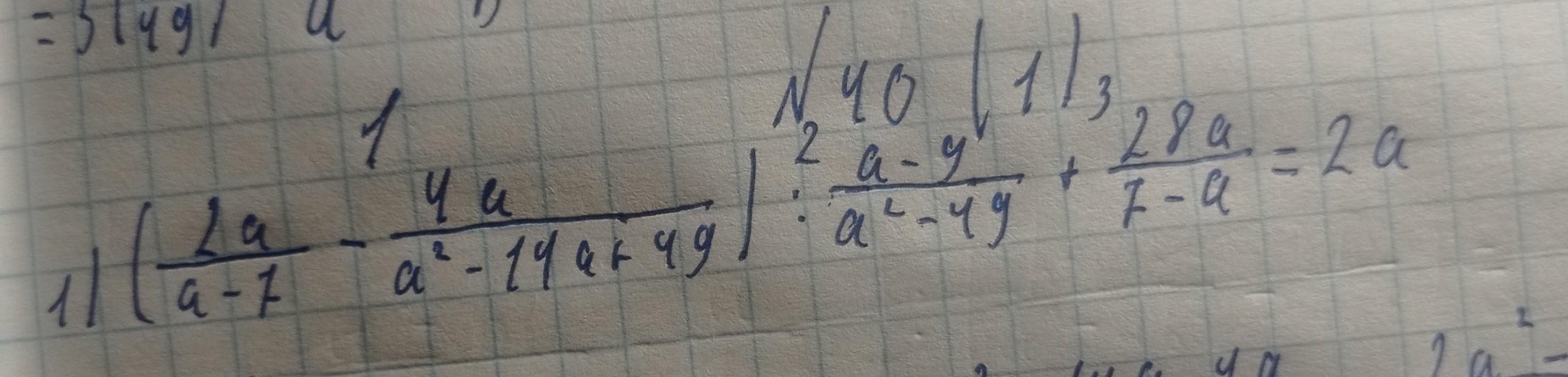
Ответы
Автор ответа:
2
Відповідь:
Пояснення:
Перетворимо ліву частину даної рівності :
1 ) 2а/( а - 7 ) - 4а/( а² - 14а + 49 ) =[ 2a( a - 7 ) - 4a ]/( a - 7 )² =
= ( 2a²- 14a - 4a )/( a - 7 )² = ( 2a²- 18a )/( a - 7 )² = 2a( a - 9 )/( a - 7 )² ;
2 ) 2a( a - 9 )/( a - 7 )² : ( a - 9 )/( a² - 49 ) = 2a(a - 9)/(a - 7 )² X
X ( a² - 49 )/( a - 9 ) = 2a( a + 7 )/( a - 7 ) ;
3 ) 2a( a + 7 )/( a - 7 ) - 28a/( a - 7 ) = ( 2a² + 14a - 28a )/( a - 7 ) =
= ( 2a² - 14a )/( a - 7 ) = 2a( a - 7 )/( a - 7 ) = 2a .
Отже , дана рівність тотожністю
Автор ответа:
0
Пояснення:
Похожие вопросы
Предмет: География,
автор: polovaangelina7
Предмет: Алгебра,
автор: Maxim28042009
Предмет: Українська мова,
автор: romaniukmatvii
Предмет: Физика,
автор: kushnardenis2002