Question

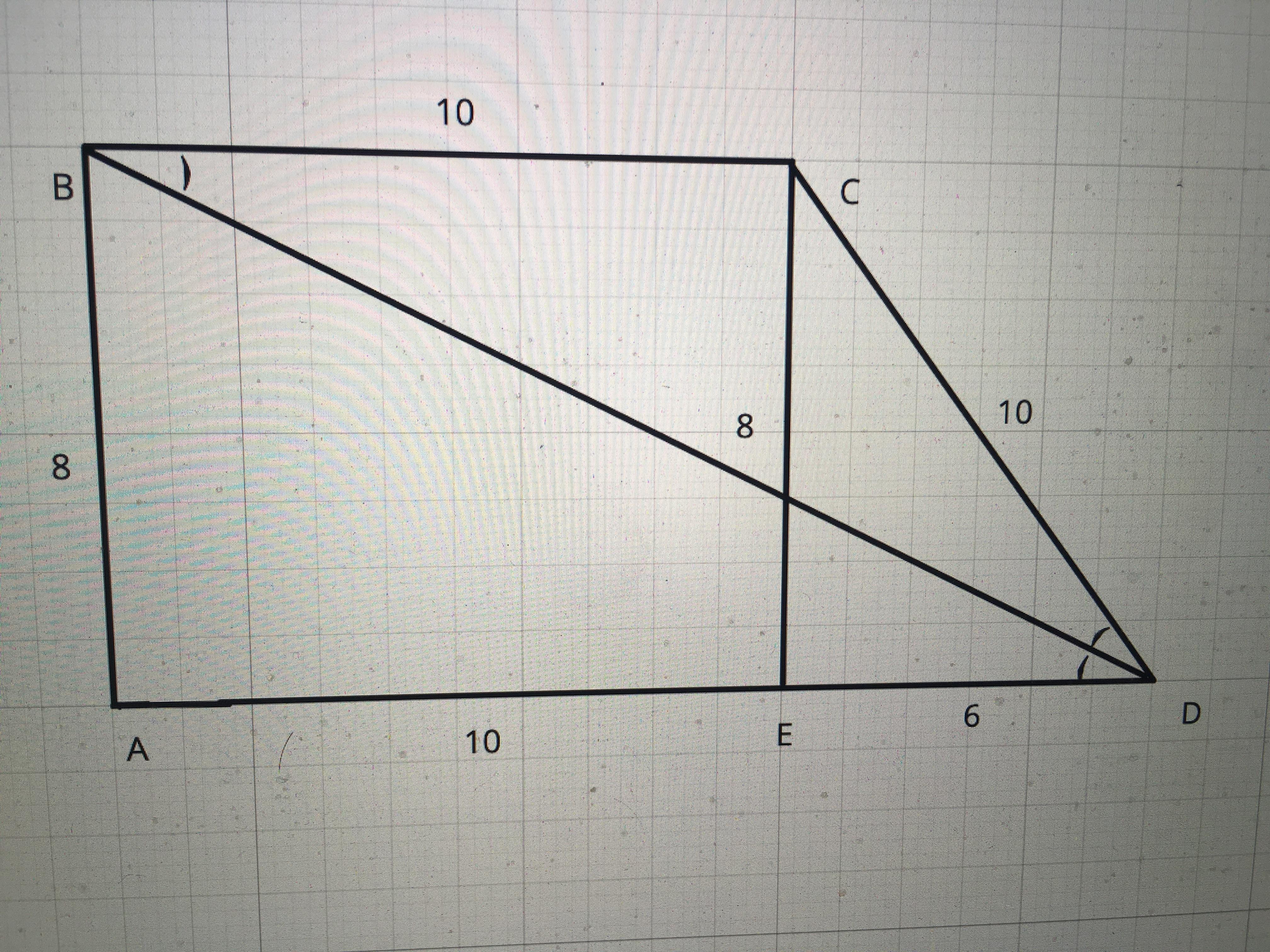
прямоугольной трапеции диагональ является биссектрисой острого угла. Найдите плошаль трапеции, если боковые стороны равны 8 см и 10 см.

Answer 1

Объяснение:

АВ=8 см ; СD=10 см

биссектриса DB отсекает равнобедреный треугольник ВСD,где ВС=СD=10 см.

S=(AD+BC)/2•СН

высота CH=AB=8 см

∆CНD -прямоугольный:

по теореме Пифагора:

НD=√(CD²-CH²)=√(10²-8²)=√36=6 см

АD=BC+HD=10+6=16 см

S=(16+10)/2•8=104 см²

ответ: 104 см²

Answer 2

Ответ:

104 см.

Объяснение:

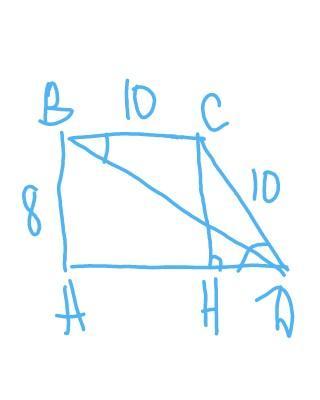
Дана прямоугольная трапеция ABCD, угол A прямой, AB=8; CD=10; угол ADB равен углу BDC.

Поскольку AD||BC, угол DBC равен углу ADB, поэтому треугольник BCD равнобедренный, BC=CD=10. Проведем высоту CE к основанию AD. Поскольку ABCE прямоугольник, AE=BC=10, EC=AB =8.

В прямоугольном треугольнике CDE гипотенуза CD=10, катет EC=8, поэтому второй катет ED=6 (если это Вам не кажется очевидным, примените теорему Пифагора). Итак, AD=AE+ED=16, поэтому площадь трапеции равна

                                $\dfrac{AD+BC}{2}\cdot AB=\dfrac{16+10}{2}\cdot 8=104.$