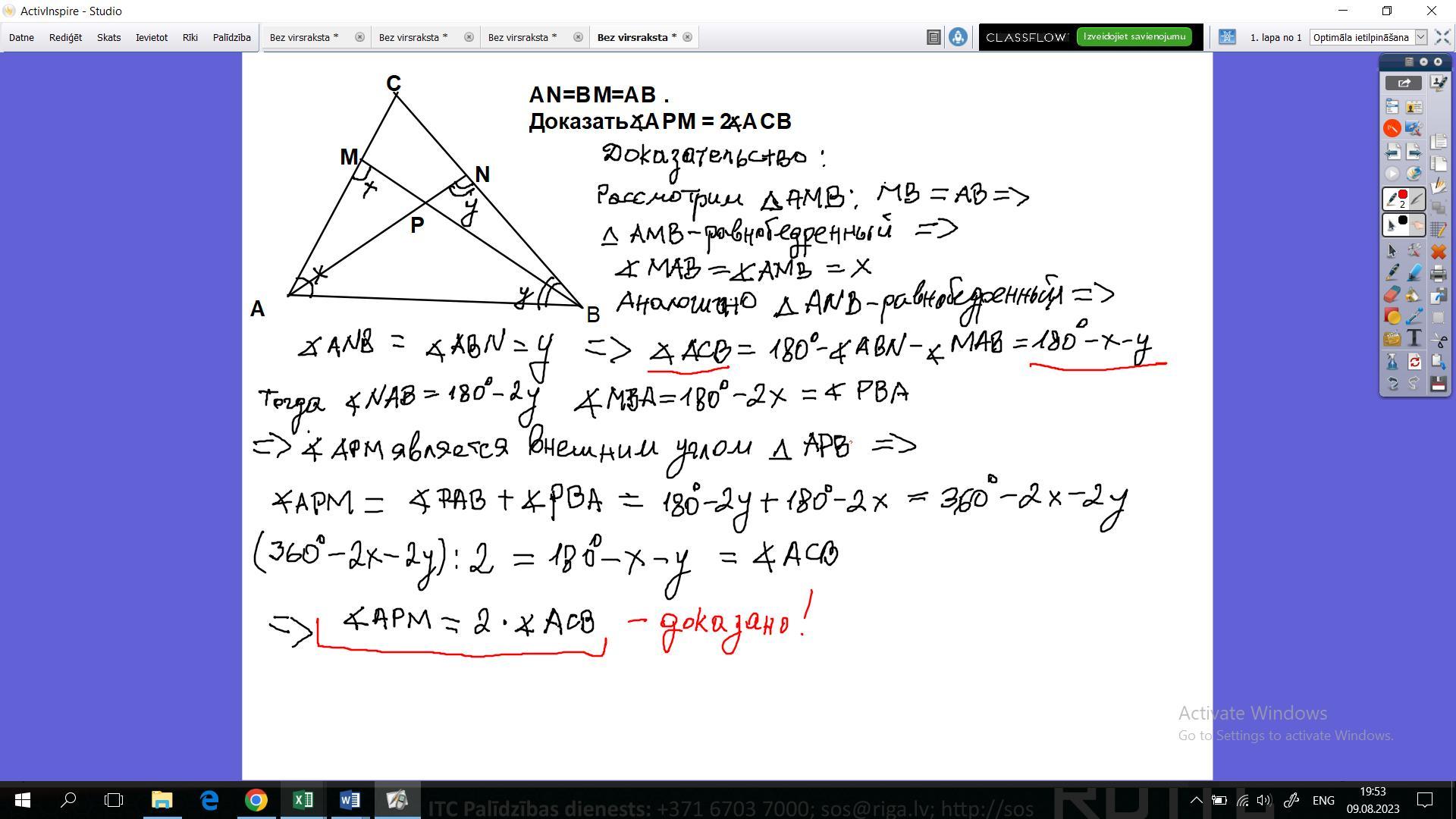
На сторонах AC і BC трикутника ABC відповідно позначили точки M і N так, що AN = BM = AB. Відрізки AN і BM пере- тинаються в точці P. Доведіть, що ∠APM = 2 ∠ACB.
Ответы
Объяснение:
Ми маємо трикутник ABC, де AN = BM = AB. Таким чином, ми маємо рівні кути ∠BAN і ∠ABM, оскільки ці кути протилежні однаковим сторонам.
Давайте позначимо ∠BAN = ∠ABM = α.
Також ми знаємо, що точки AN і BM перетинаються в точці P. Це означає, що кути ∠APB і ∠BPA в сумі дають 180° (оскільки це внутрішні кути ламаної APBN). З цього можна записати:
∠APB + ∠BPA = 180°
Ми також помітимо, що ∠APB = ∠BAN + ∠ABM, оскільки ці кути стираються дугами того самого кола.
∠APB = α + α = 2α
Замінивши це значення в рівнянні ∠APB + ∠BPA = 180°, ми отримаємо:
2α + ∠BPA = 180°
Відси ми можемо виразити ∠BPA:
∠BPA = 180° - 2α
Але ми помітили, що ∠BAN = ∠ABM = α, і оскільки AN = BM, трикутники ANP і BMP є рівнобедреними, і відповідні основи в цих трикутниках рівні.
Тепер ми розглянемо трикутник AMP. Оскільки AM = MP (вони є радіусами одного кола), то ∠AMP = ∠MAP, тобто кут між стороною трикутника і радіусом дорівнює куту між іншою стороною трикутника і цим самим радіусом.
Отже, ∠AMP = ∠BPA = 180° - 2α.
Також ми помітили, що ∠BAN = α, і таким чином, ∠ACB = α.
Тепер ми можемо зробити висновок:
∠APM = ∠AMP - ∠ACB = (180° - 2α) - α = 180° - 3α
Але ми знаємо, що ∠ACB = α, тому:
∠APM = 180° - 3α = 2α
Отже, ми довели, що ∠APM = 2∠ACB.
Ответ:
Объяснение:
См доказательство