Предмет: Алгебра,
автор: mgisminy
решите системы уравнений методом замены
Приложения:
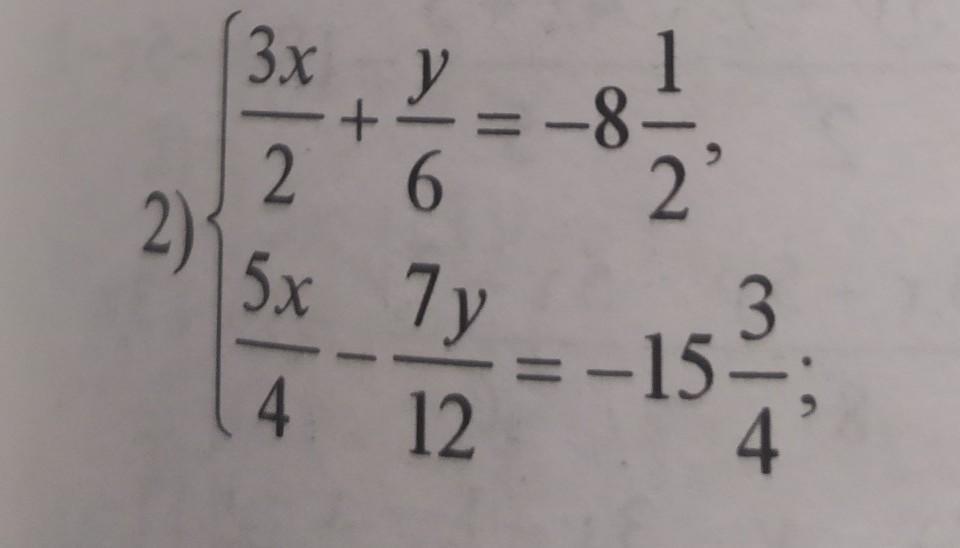
Ответы
Автор ответа:
0
Ответ:
Если надо решить методом замены , то удобно заменить дроби на новые переменные .
Решаем систему методом сложения .
Сделаем обратную замену .
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: Stacyko11
Предмет: Геометрия,
автор: isiisiaisiksi
Предмет: Химия,
автор: VladosUKRAINE
Предмет: Математика,
автор: zhadyratursynbek
Предмет: Английский язык,
автор: serenkijila