Question

У прямокутному трикутнику катет, прилеглий до кута 30⁰
,, дорівнює 18 см .
Знайдіть довжину бісектриси трикутника, проведеної до даного катета.

Answer 1

Відповідь:   12 см .  

Пояснення:

У прямок.  ΔАВС  ∠А = 30° ;  ∠С = 90° .  ∠В = 90° - ∠А = 90°- 30° = 60°.

ВК - бісектриса ∠В , тому  ∠СВК = ∠АВК= 1/2 ∠В = 1/2 * 60° = 30° .

  У прямок. ΔАВС  АВ = 2* ВС , бо ∠А = 30° .  АК = ВК , бо у ΔАВК

два рівні кути . За Т. Піфагора  АВ² = ВС² + АС² ;

   ( 2 ВС )² = ВС² + 18² ;

     3 ВС² = 18² ;

        Вс= 18/√3 = 6√3 ( см ) .  АВ = 2 * 6√3 = 12√3( см ) .

  ∠AKB = 180° - 60° = 120° . Із ΔАКВ за Т. косинусів

   AB² = AK² + BK² - 2* AK * BK* cos120° ;

   2 *BK² +  2 *BK² * 1/2 = ( 12√3 ) ² ;

   3 *BK² = 12² * 3 ;

        BK² = 12² ;

        BK = 12 cм , ( ВК > 0 ) .

   В  -  дь :  12 см .              

 

Answer 2

Ответ:

Длина биссектрисы треугольника, проведенной к данному катету, равна 12 см.

Объяснение:

В прямоугольном треугольнике катет, прилегающий к углу 30⁰, равно 18 см. Найдите длину биссектрисы треугольника, проведенной к данному катету.

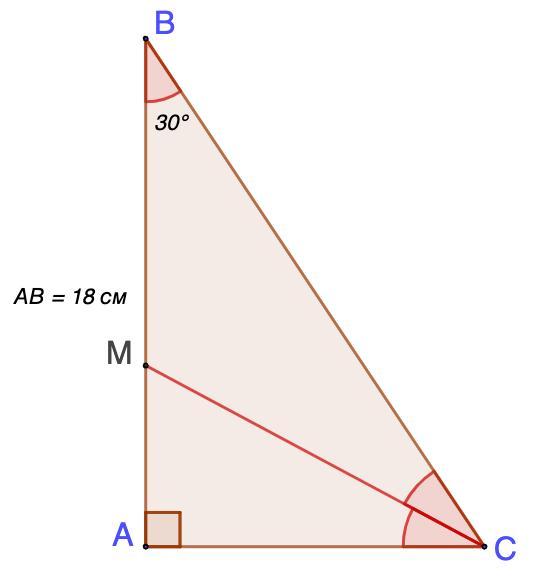
Дано: ΔАВС - прямоугольный;

∠В = 30°; АВ = 18 см;

СМ - биссектриса.

Найти: СМ.

Решение:

Рассмотрим ΔАВС - прямоугольный.

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle tg\angle B=\frac{AC}{AB} \\\\tg\;30^0=\frac{AC}{18}\;\;\;\Rightarrow \;\;\;AC=18\cdot \frac{\sqrt{3} }{3}=6\sqrt{3} \;_{(CM)}$

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠С = 90° - 30° = 60°

СМ - биссектриса

⇒ ∠ВСМ = ∠МСА = 30°

Рассмотрим ΔАМС - прямоугольный.

• Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle cos\angle MCA=\frac{AC}{MC}\\ \\cos\;30^0=\frac{6\sqrt{3} }{MC} \;\;\;\Rightarrow \;\;\;MC=\frac{6\sqrt{3}\cdot 2 }{\sqrt{3} } =12\;_{(CM)}$

Длина биссектрисы треугольника, проведенной к данному катету, равна 12 см.