Очень нужна помощь
1) Сколькими способами можно сложить 6 томов энциклопедии так, чтобы 1-й том не оказался выше 2-го?
Ответ должен быть 360.
2) Найти n,то что на фото.
В ответе n должно равняться 15.
3) Найти значение выражения (a^3)-(a^-3), ecли a-(a^-1)=4
Ответ должен получиться 76.
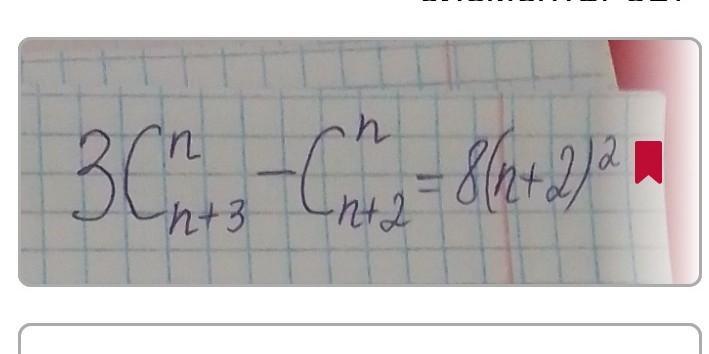
Ответы
1) Сколькими способами можно сложить 6 томов энциклопедии так, чтобы 1-й том не оказался выше 2-го?
1 случай, первый том находится на первой полке, тогда остальные 6 - 1 = 5 томов мы можем расставить как угодно, т.е 5! = 120 способами
2 случай, первый том находится на второй полке, для второго тома остается 5 - 1 = 4 места, а остальные 4 тома можно расставить 4! = 24 способами, тогда всего есть 24·4= 96 способов удовлетворяющих условию задачи
3 случай, по той же аналогии, (5 - 2)·4! = 72 способа
4 случай, (5-3)·4! = 48 способов
5 случай, (5-4)·4! = 24 способа
6 случая нет, т.к оказавшись на последней полке, 1-й том будет в любом случае ниже второго
Итого : 120 + 96 + 72 + 48 + 24 = 24·(5 + 4 + 3 + 1) = 24·15 = 360 способов
2) Найти n, если
Корень в первой скобке не подходит, т.к n = - 2 ∉ N, рассматриваем вторую
По теореме Виета
n₁ = 15 , n₂ = - 2 ∉ N
⇒ n = 15 - корень
3) Найти значение выражения (a^3)-(a^-3), ecли a-(a^-1)=4
По формуле разностей кубов