Со станции А и В вышли два поезда навстречу друг другу, причем второй из них вышел на полчаса позже первого. Через 2 часа после выхода первого поезда расстояние между поездами составляло 19/30 всего пути между А и В. Продолжая движение, они встретились на середине пути между А и В. Сколько времени потребуется каждому поезду, чтобы пройти весь путь между конечными станциями?
Ответы
Ответ:
10 часов потребуется первому поезду и 9 часов потребуется второму поезду, чтобы пройти весь путь между конечными станциями.
Пошаговое объяснение:
Со станции А и В вышли два поезда навстречу друг другу, причем второй из них вышел на полчаса позже первого. Через 2 часа после выхода первого поезда расстояние между поездами составляло 19/30 всего пути между А и В. Продолжая движение, они встретились на середине пути между А и В. Сколько времени потребуется каждому поезду, чтобы пройти весь путь между конечными станциями?
Примем расстояние АВ за 1.
Пусть скорость первого поезда - V₁ = х км/ч, скорость второго поезда -
V₂ = у км/ч.
Вспомним формулы:
S = Vt; V = S:t; t = S:V
1.
- Со станции А и В вышли два поезда навстречу друг другу, причем второй из них вышел на полчаса позже первого.
⇒ второй поезд был в пути от В до К на 0,5 ч меньше, чем первый поезд от А до М.
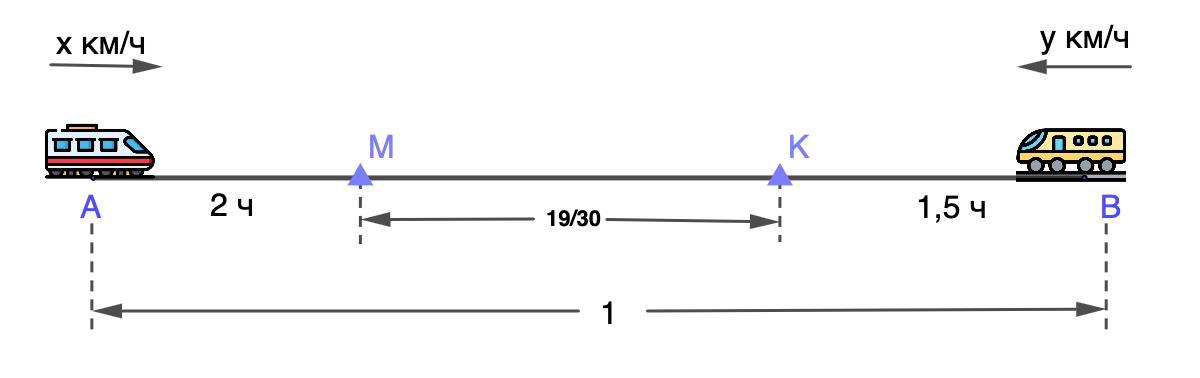
- Через 2 часа после выхода первого поезда расстояние между поездами составляло 19/30 всего пути между А и В.
⇒ первый поезд прошел АМ за 2 часа, второй поезд прошел ВК за 1,5 часа.
(часть пути)
2.
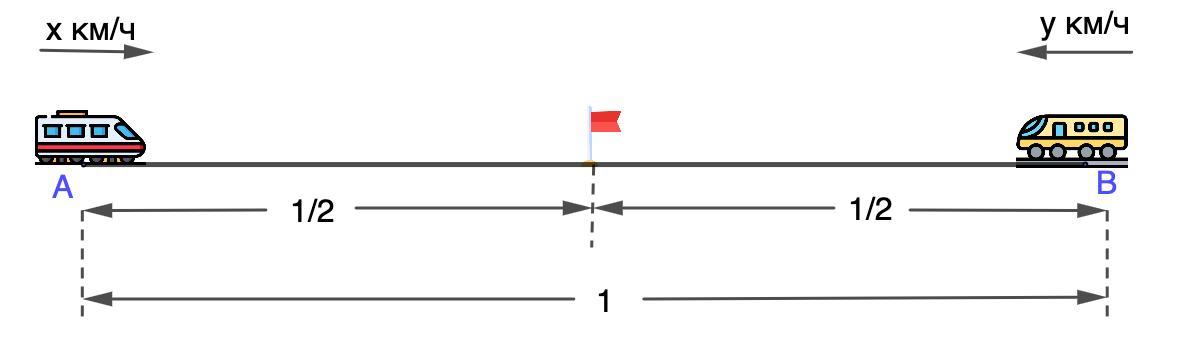
- Продолжая движение, они встретились на середине пути между А и В.
⇒ каждый поезд до встречи прошел по 1/2 части пути.
Время первого поезда до встречи равно:
(ч)
Время второго поезда до встречи равно:
(ч)
- ...причем второй из них вышел на полчаса позже первого.
Составим уравнение:
Составим систуму из (1) и (2):
Решим методом подстановки. Из первого уравнения выразим x и подставим во второе уравнение:
y₂ - не подходит по условию задачи.
Нашли скорость первого поезда - 1/10 часть пути/ч; скорость второго поезда - 1/9 часть пути/ч.
Расстояние равно 1. Можем найти время, которое потребуется каждому поезду, чтобы пройти весь путь между конечными станциями:
(ч)
(ч)