Предмет: Алгебра,
автор: kokoko2222
Вопрос в фото докажите что...при всех действительных значениях...
Приложения:
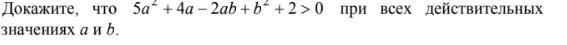
kokoko2222:
Отзовитесь, кто-то отыетит?
Ответы
Автор ответа:
2
Ответ:
Сумма квадратов неотрицательна, то есть больше, чем -1. Значит для любых a,b неравенство выполняется.
Автор ответа:
0
Неравенство верно при любых a и b, поскольку левая часть всегда положительно
Похожие вопросы
Предмет: Українська мова,
автор: spakovalina428
Предмет: География,
автор: Аноним
Предмет: Литература,
автор: yanamartynukua
Предмет: Математика,
автор: МАКСИМ23458657
Предмет: Математика,
автор: flefll