Предмет: Алгебра,
автор: V9ova
Здравствуйте, подскажите пожалуйста как решать такие неравенства вида
||f| - |g|| >= |t|
Приложения:
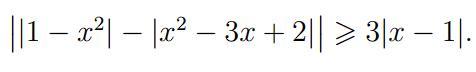
hderyb:
|a|≥b есть совокупность a>b, a≤-b, от первого модуля слева избавились, а дальше и общий множитель выносится
не напишу
( - беск ; -1 ] , {1} , [2 ; + беск)
напишу , есть простое решение , почти устное
Давайте
Берите
|a| < |b| < => |a|^2 < |b|^2 < = > a^2 - b^2 < 0 < = > (a -b) ( a +b) < 0 - примерно так надо решать подобные неравенства
а здесь и в квадрат можно было не возводить : | |a| - |b| | ≥ | a + b| < => ab <= 0 , так как при этом условии левая часть равна правой , а все остальные варианты не подходят ( то есть вторая строка моего решения лишняя )
Ответы
Автор ответа:
1
Ответ:
Объяснение:
1 - x² = a ; x² - 3x +2 = b , | |a| - |b| | ≥ | a + b| ⇔ ( | |a| - |b| | )² ≥ | a + b| ² ⇔
a² - 2 |ab| +b² ≥ a² +2ab + b² ⇔ ab +|ab| ≤ 0 ⇔ ab ≤ 0 ⇔
(1 - x²) ( x² -3x +2) ≤ 0 ⇔ (x - 1)² (x+1) (x -2) ≥ 0 ⇔ x ∈ (- ∞ ; -1 ) ∪ {1} ∪ [ 2 ; +∞ )
Похожие вопросы
Предмет: Українська література,
автор: Аноним
Предмет: Другие предметы,
автор: gizaliza2
Предмет: Информатика,
автор: picka4ywckaa
Предмет: Математика,
автор: gnasta086
Предмет: Математика,
автор: veprvepr