розв'язати рівняння.
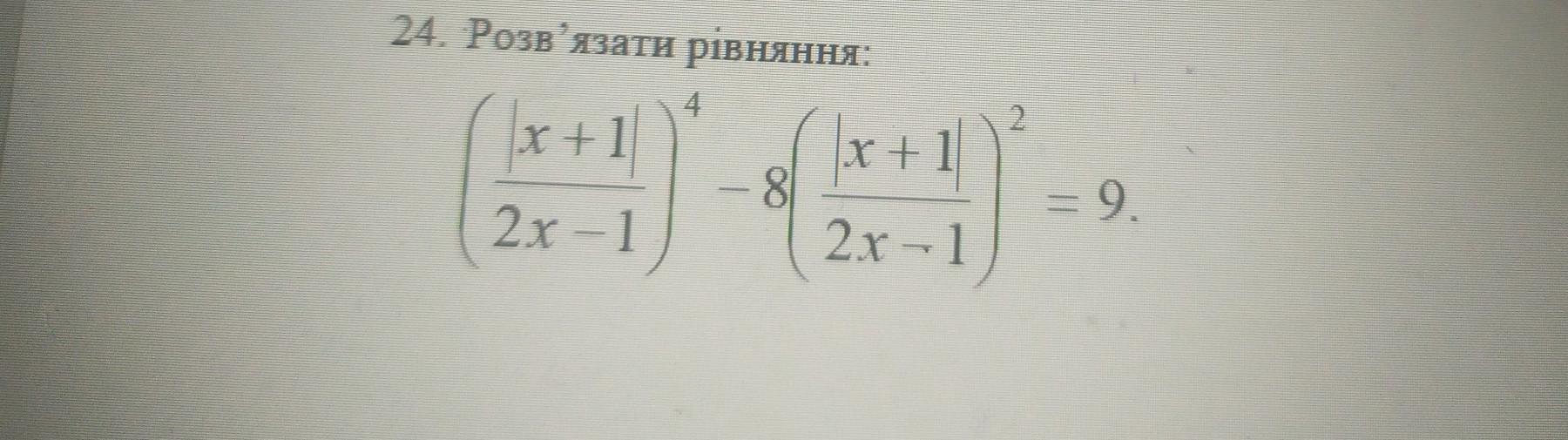
Ответы
Відповідь:
Пояснення: Всі пояснення в дужках не переписуємо!
(перед нами дві однакові дужки, тому ми можемо зробити заміну цілої дужки. замінемо другу на а)
Замінемо .( одразу зауважимо , що а буде завжди більше рівно 0, бо квадрат від'ємним не буває.), де а≥0.
а²-8а= 9. ( перенесемо 9 вліво і получимо квадратне рівняння)
а²-8а-9=0;
За теоремою Вієта а₁= -1; а₂=9., так як а₁<0 ( то цей корінь не беремо до уваги !) а=9
(тепер вертаємось до дужки, що ми замняли)
(опускаємо квадрати)
( розуміємо, що ліва частина може бути рівна 3 або -3)
1) , де х≠ 0,5 ( бо знаменник не може бути рівний 0)
|x+1|=-3(2x-1);
|x+1|= -6х+3; (щоби розкрити модуль розуміємо, що вираз під модулем може бути від'ємни і додатнім)
а) (підмодульний вираз більше нуля)
х+1= -6х+3;
х+6х=3-1;
7х=2;
х=2:7;
б) (підмодульний вираз менше нуля)
-(х+1)=-6х+3;
-х+6х=3+1;
5х=4;
х=4:5;
х₂=0,8
!!!!!!2)( Другий варіант коли ліва частина заміни =+3 то не варто би було писати, бо там корені співпадають!!!!!! Але розпишу тут, для вас )
в) (підмодульний вираз більше нуля)
x+1=6x-3;
x-6x=-3 -1;
-5x=-4
x=-4:(-5);
x₃=0,8
г) (підмодульний вираз менше нуля)
-(х+1)= 6х-3;
-х-6х=-3+1;
-7х=-2