Question

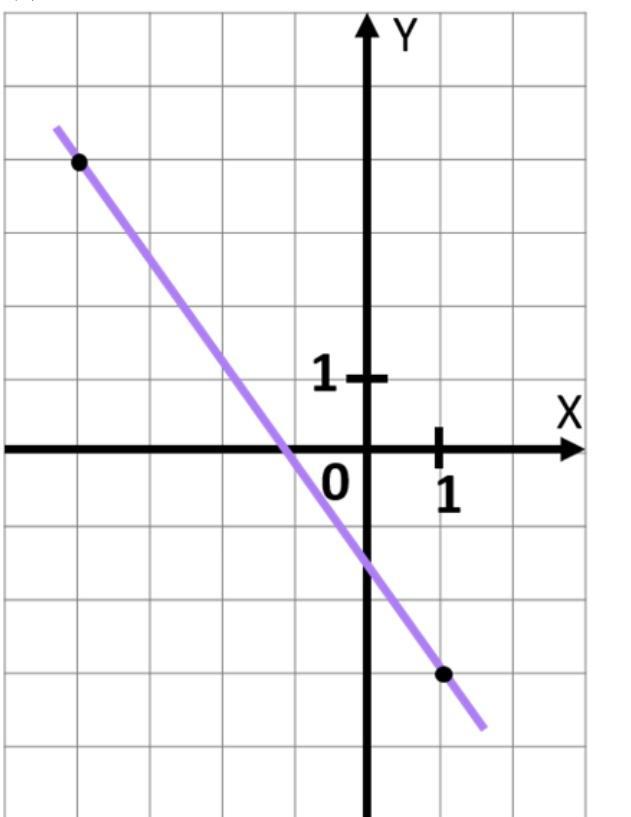
На рисунке изображен график функции f(x)=kx+b. Найдите значение x, при котором f(x) = -140,2.

Answer 1

Ответ:

Значение x при котором f(x)=-140,2 равно 99, тоесть

$x = 99$

Объяснение:

График функции f(x)=kx+b это уравнение прямой линии. Из рисунка видно, что прямая линия проходит через две точки с координатами (-4;4) и (1;-3). Эти две точки мы назовем A(-4;4) и B(1;-3) где

x1=-4

x2=1

y1=4

y2=-3

Найдем уравнение прямой линии, проходящей через две точки A(-4;4) и B(1;-3) по формуле: (1)

$\frac{x - x1 \\ }{x2 - x1} = \frac{y - y1}{y2 - y1}$

Подставим значения x1; x2; y1; y2 в уравнение (1). Имеем:

$\frac{x - ( - 4)}{1 - ( - 4)} = \frac{y - 4}{ - 3 - 4}$

$\frac{x + 4}{1 + 4} = \frac{y - 4}{ - 3 - 4}$

$\frac{x + 4}{5} = \frac{y - 4}{ - 3 - 4}$

$\frac{x + 4}{5} = \frac{y - 4}{ - 7}$

$\frac{y - 4}{ - 7} = \frac{x + 4}{5}$

$5(y - 4) = - 7(x + 4)$

Раскроем скобки и приведем подобные слагаемые. Имеем:

$5(y - 4) = - 7(x + 4)$

$5y - 20 = - 7x - 28$

$5y = - 7x - 28 + 20$

$5y = - 7x - 8$

$y = - \frac{7}{5} x - \frac{8}{5}$

Проверка:

Подставим координаты точки A)-4;4) в уравнение прямой:

$4 = - \frac{7}{5} \times ( - 4) - \frac{2}{5}$

$4 = \frac{28}{5} - \frac{8}{5}$

$4 = \frac{20}{5}$

$4 = 4$

$4 - 4 = 0$

Подставим координаты точки B(1;-3) в уравнение прямой. Имеем:

$- 3 = - \frac{7}{5} \times 1 - \frac{8}{5}$

$- 3 = - \frac{7}{5} - \frac{8}{5}$

$- 3 = - \frac{15}{5}$

$3 = \frac{15}{5}$

$3 = 3$

$3 - 3 = 0$

$0 = 0$

Следовательно, точки A(-4;4) и B(1;-3) принадлежат графику функции

$y = - \frac{7}{5} x - \frac{8}{5}$

По условию задачи

$f(x) = - 140.2$

Подставим это значение вместо y в уравнение графика функции. Имеем уравнение:

$- 140.2 = - \frac{7}{5} x - \frac{8}{5}$

Найдем значение x. Имеем:

$- 140.2 = - \frac{7}{5} x - \frac{8}{5}$

$- \frac{7}{5} x - \frac{8}{5} = - 140.2$

$- 1.4x - 1.6 = - 140.2$

$- 1.4x = - 140.2 + 1.6$

$- 1.4x = - 138.6$

$1.4x = 138.6$

$x = \frac{138.6}{1.4}$

$x = 99$

Ответ:

Значение x при котором f(x)=-140,2 равно 99

тоесть

$x = 99$