Question

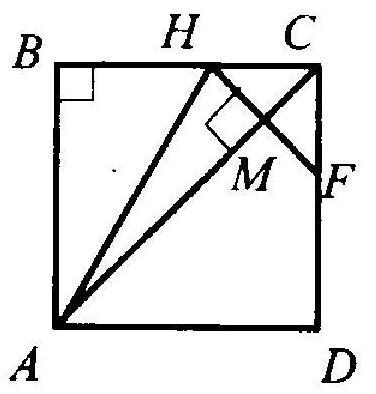
В квадрате ABCD провели диагональ AC и отметили на ней точку M так, что AM = AB.
Через точку M провели прямую, перпендикулярную AC, которая пересекает сторону BC
в точке H. Докажите, что BH = HM = MC.
Срочно!!

Answer 1

1. Треугольник HMC является прямоугольным и равнобедренным, так как угол HCM равен 45°. Поэтому HM = MC.

2. Треугольники ABH и AMH равны по катету и гипотенузе, так как AM = AB и AH — общая. Следовательно, BH = HM.

3. Из пункта 1 следует, что HM = MC, а из пункта 2 следует, что BH = HM. Таким образом, BH = HM = MC.