Question

Пожалуйста помогите!!
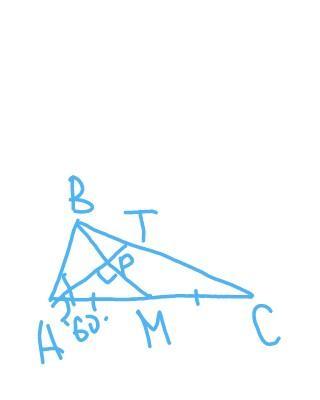
В треугольнике АВС биссектриса АТ, перпендикулярна медиане ВМ пересекает ее в точке Р. Найдите сторону ВС, если угол А=60 градусов и РМ =8 см .

Answer 1

Пошаговое объяснение:

∆АPM - прямоугольный:

∠РАМ=∠ВАР=∠А:2=60:2=30°,т.к АТ - биссектриса.

катет лежащий против угла 30° равен половине гипотенузы:

АМ=2•РМ=2•8=16 см

cos∠PAM=AP/AM ;

AP=AM•cos30=16•√3/2=8√3 см

АС=2•АМ=2•16=32 см ,т.к ВМ - медиана.

∆АВР:

cos∠BAP=AP/AB ;

AB=AP/cos30=8√3/(√3/2)=16 см

∆АВС:

из теоремы косинусов:

ВС=√(АС²+АВ²-2•АС•АВ•cos∠A)=

=√(32²+16²-2•32•16•cos60)=

=√(1024+256-1024•1/2)=√768=16√3 см

ответ: D) 16√3 см