Предмет: Алгебра,
автор: Аноним
Решить задание на скриншоте.
Приложения:
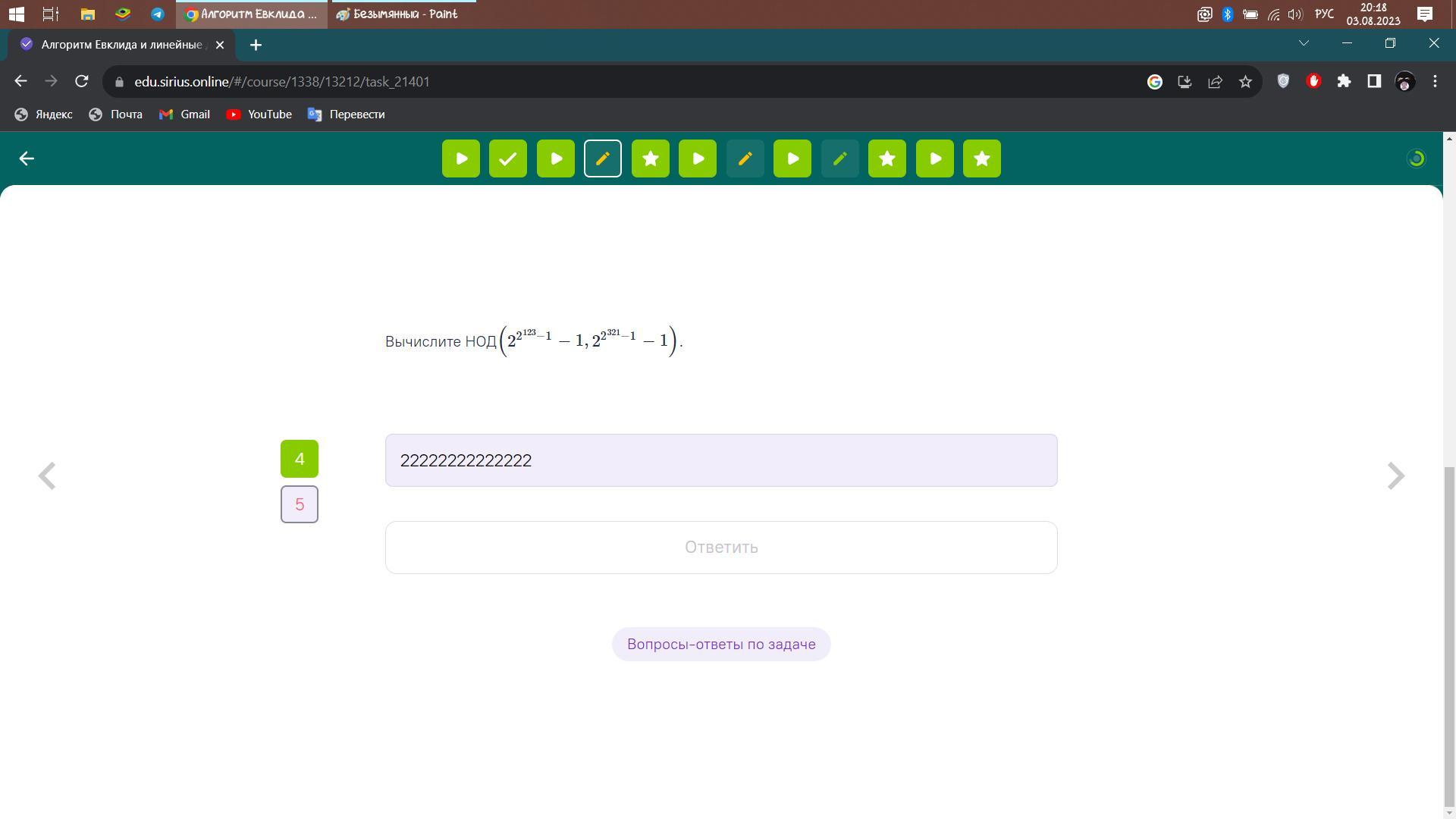
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Воспользуемся теоремой
Следовательно
По той же теореме
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Другие предметы,
автор: limochikhaha
Предмет: Информатика,
автор: gomanoid32208
Предмет: Алгебра,
автор: nataborshch01
Предмет: Геометрия,
автор: kosterinmihail658