Предмет: Математика,
автор: yhyhyhhy25
Дан треугольник АВС. Известен угол В = 30°, угол С = 45° и сторона АВ = 12 см. Найти сторону ВС.
Ответы
Автор ответа:
1
Ответ: 16.4 см.
Пошаговое объяснение:
Угол А=180*-(30*+45*) = 105* (градусов)
По т. синусов
a/sinA=b/sinB=c/sinC.
AB=c=12 см.
sinA=sin105* = 0.966.
sinC=sin45* = 0.707.
a/sin(105*) = c/sin(45*);
BC=a=12*0.966/0.707.
BC=16.4 см.
Автор ответа:
1
Ответ:
6(1+√3).
Пошаговое объяснение:
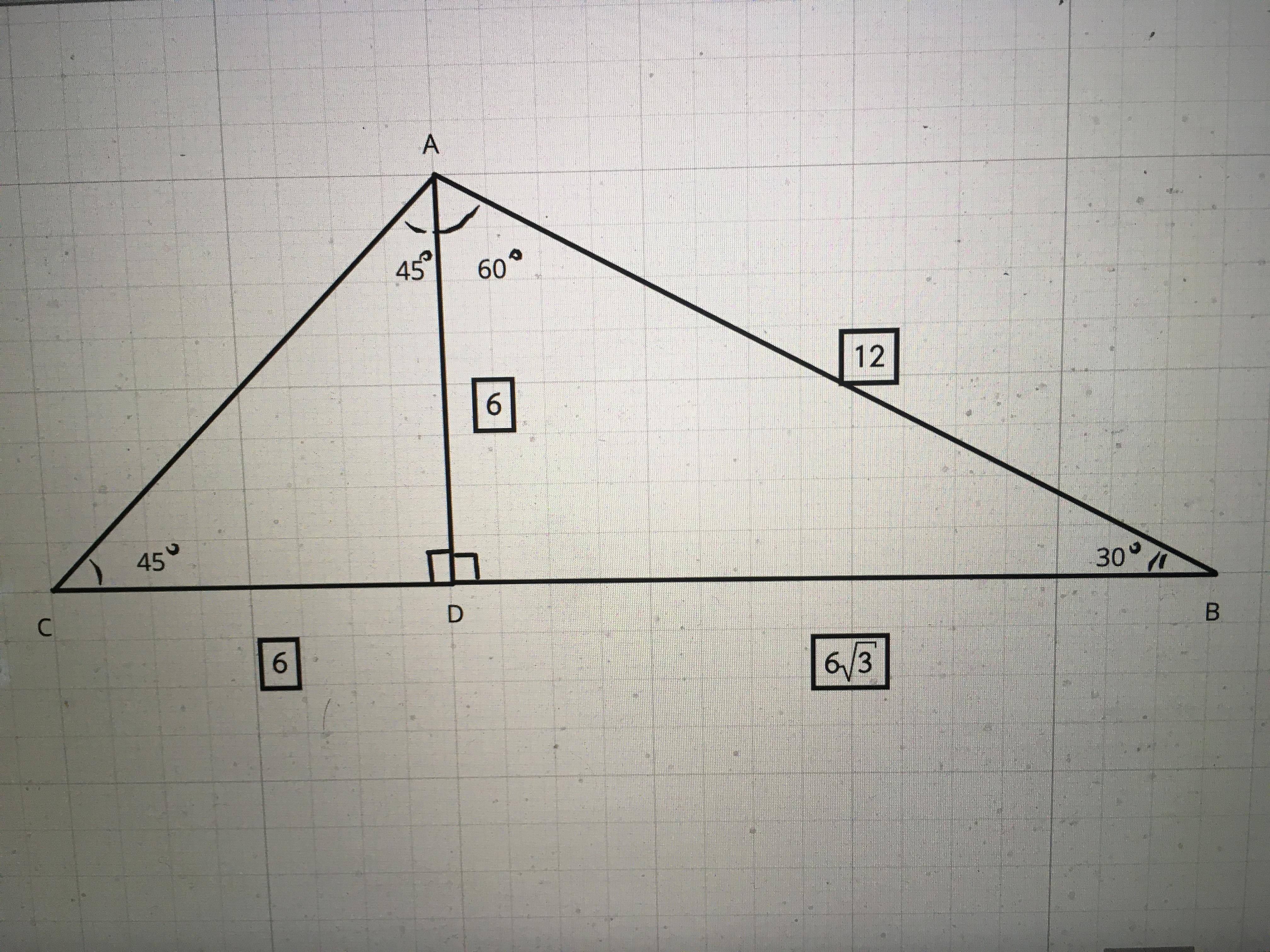
Опустим высоту AD на сторону BC. Получаем два прямоугольных треугольника ABD и ACD.
В первом из них острые углы равны 30 и 60 градусов, поэтому AD=AB/2=12/2=6 (катет, лежащий против угла в 30 градусов, равен половине гипотенузы); BD=AD·tg 60°=6√3.
Второй из них - равнобедренный прямоугольный, поэтому CD=AD=6.
Вывод: BC=BD+CD=6√3+6.
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: sofiabanderix18
Предмет: Українська мова,
автор: Аноним
Предмет: Математика,
автор: qwercoff
Предмет: Алгебра,
автор: gjcc
Предмет: Математика,
автор: vivey14