Question

Решить задачу на скриншоте.

Answer 1

Ответ:

Существует  21 — целое   решение уравнения 97x−45y=3, при которых хотя бы одно из чисел x и y является положительным трёхзначным числом

Объяснение:

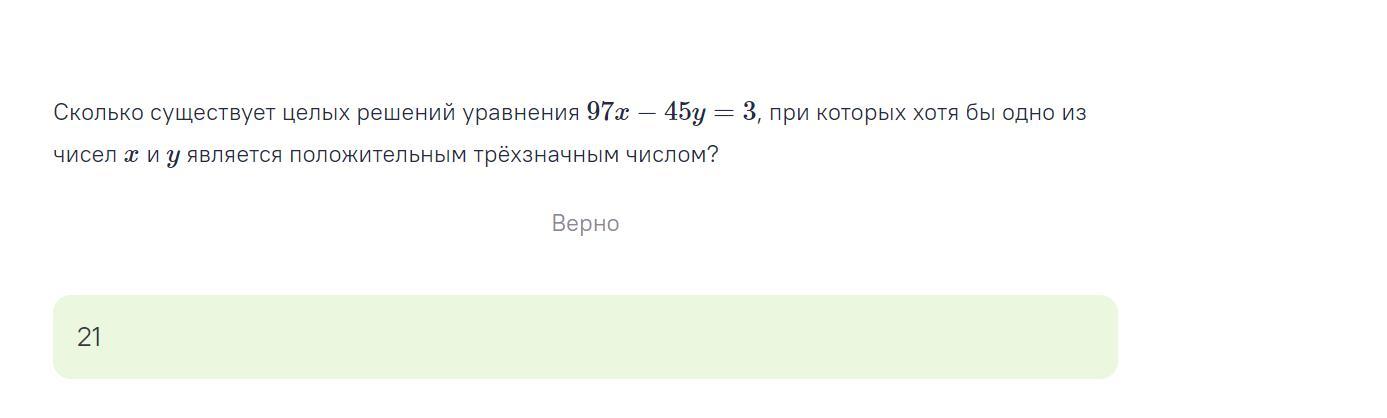
Сколько существует целых решений уравнения 97x−45y=3, при которых хотя бы одно из чисел x и y является положительным трёхзначным числом?

Теорема. Линейное диофантово уравнение ax+by = c

с неизвестными x  и y имеет решение тогда и только тогда, когда
c ⫶ НОД(a,b) , c ≥ НОД(a,b)

97x - 45y = 3

Введем обозначение y₁ = 3y

97x  - 15y₁ = 3

Из выше указанной теоремы, 3 ⁝ НОД(x , y₁) ⇒ x ⋮ 3, при этом сам y необязательно кратен трем, таким образом $x = 3k , k \not \vdots~ 3$ , поскольку в случаи кратности k к трем, НОД  будет равен 9, а как нам известно правая часть уравнения  кратна только 3

Тогда мы получим новое  уравнение

97·3k - 45y = 3 | : 3

97k - 15y = 1

*97 = 15·6 + 7 ⇒ 7 = 97 - 15·6

** 1 = 15 - 2·7

Подставив следствие из * во ** , и получим что :

1 = 15  - 2 · (97 - 15·6) = 13·15 - 2·97

Значит,  уравнение 97k - 15y = 1  имеет корень k₀ = -2 ,  y₀ = -13

97k₀ - 15y₀ = 1

97(k₀ +15) - 15(y₀ + 97) = 1

Соответственно всё множество решений уравнения 97k - 15y = 1 — это пары вида k = -2 + 15m , y=-13 +97m  для произвольных целых m

Вспомним что  x = 3k  ⇒ исходное уравнение имеет множество целых решений :

3k = x  = -6 + 45m , y=-13 +97m

Ну  и напоследок  просто остается найти такие m, при которых  хотя бы одно   из чисел x и y является трехзначным, т.е

Случаи при которых x - трехзначный

100 ≤ x ≤ 999

100 ≤ -6 + 45m ≤ 999

$\dfrac{106}{45} \leqslant m \leqslant \dfrac{1005}{45} \\\\\\ 2 \dfrac{16}{45} \leqslant m \leqslant 22 \dfrac{15}{45}$

Поскольку m - целое, то   $3\leqslant m_x\leqslant 22$

Случаи при которых y - трехзначный

100 ≤ y ≤ 999

100 ≤ -13 +97m ≤ 999

$1\dfrac{16}{97} \leqslant m \leqslant 10 \dfrac{42}{97}$

Из-за целостности  получаем что     $2\leqslant m_y\leqslant 10$

В совокупности

$(m_x \cup m_y ) \in [2 ~ ;~ 22 ~]$

Итак,  существует 22 - 2 + 1  = 21 — целое   решение уравнения 97x−45y=3, при которых хотя бы одно из чисел x и y является положительным трёхзначным числом