Предмет: Алгебра,
автор: Аноним
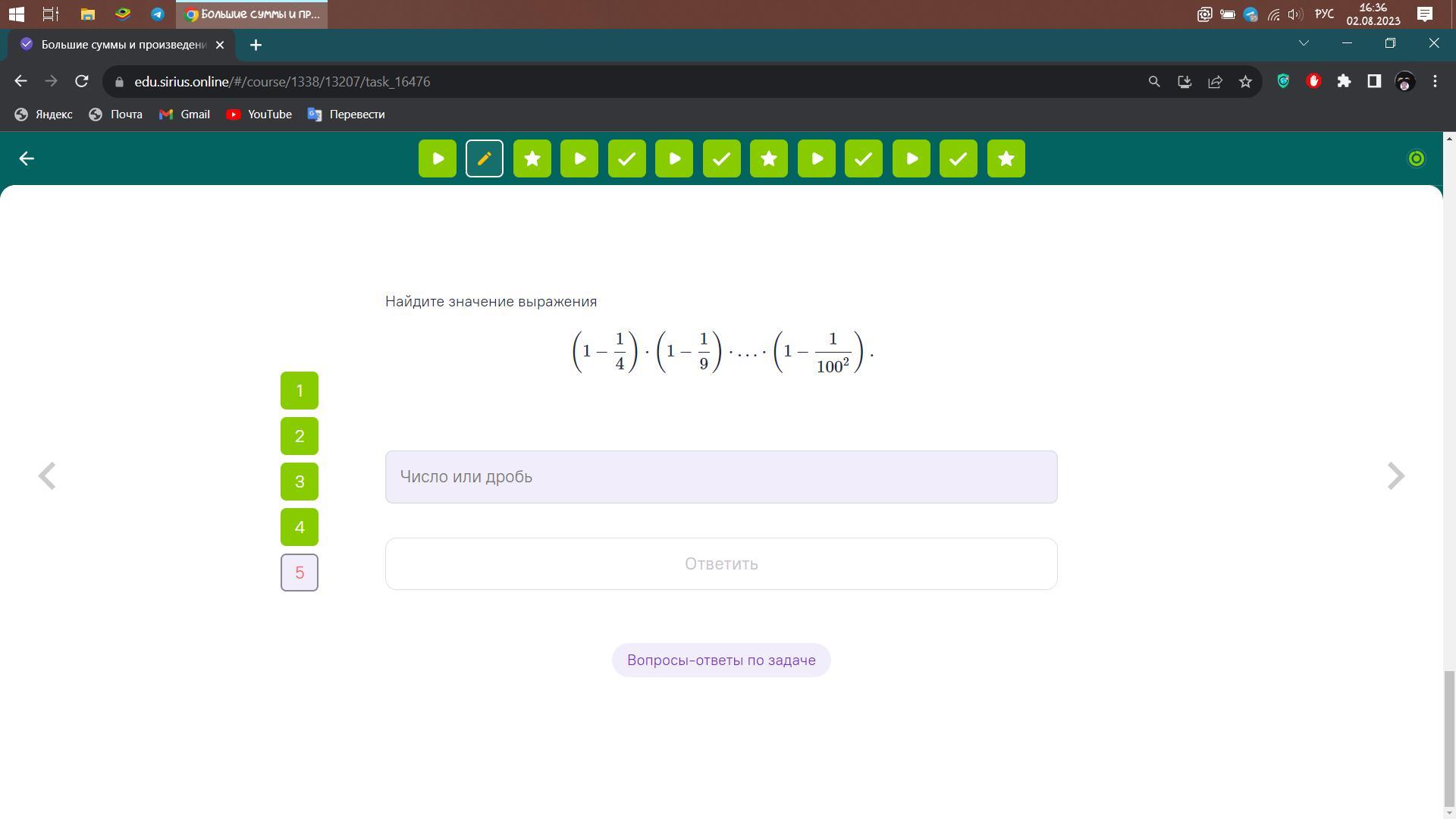
Найти значение выражения на скриншоте.
Приложения:
Ответы
Автор ответа:
1
Ответ:
0.505
Объяснение:
=
leprekon882:
Ответ: 101/200
Извиняюсь, исправил.
Автор ответа:
1
101/200
#####################
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: 555ai555
Предмет: История,
автор: Shapkarina
Предмет: Українська мова,
автор: vika20101903vika
Предмет: Химия,
автор: aaaadimaaa
Предмет: Математика,
автор: ryabinkinaveronica