Для определения вероятности отклонения относительной частоты наступления события от вероятности его появления в одном(!) опыте не более чем на заданную величину используют формулу
Пожалуйста, с объяснением или источником
Формулы, которые не являются корректным ответом вообще существуют и используются где-то? Или тут один верный ответ, а остальные - абракадабра?
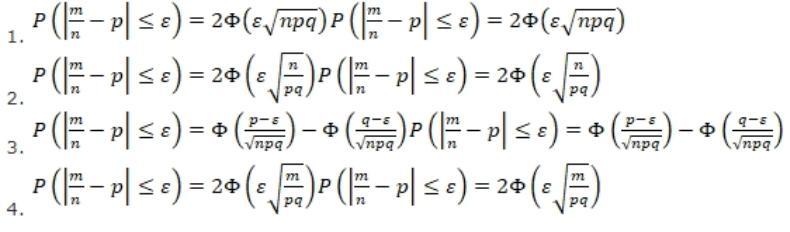
Ответы
Ответ:
Ответ 2 больше всего подходит
Пошаговое объяснение:
Для определения вероятности отклонения относительной частоты наступления события от вероятности его появления в одном(!) опыте не более чем на заданную величину, используют две основные формулы: неравенство Чебышёва и неравенство Хёфдинга. Для обеих формул существуют различные вариации, которые применяются в различных ситуациях.
Неравенство Чебышёва:
Пусть X - случайная величина с математическим ожиданием E(X) и дисперсией Var(X). Тогда для любого положительного числа ε неравенство Чебышёва имеет следующий вид:
P(|X - E(X)| >= ε) <= Var(X) / ε^2.
Неравенство Хёфдинга (первая версия):
Пусть X1, X2, ..., Xn - независимые и одинаково распределенные случайные величины, каждая из которых имеет значения в интервале [a, b]. Пусть S_n = (X1 + X2 + ... + Xn) / n - относительная частота наступления события. Тогда для любого положительного числа ε неравенство Хёфдинга имеет следующий вид:
P(|S_n - E(S_n)| >= ε) <= 2e^(-2nε^2 / (b-a)^2).
Неравенство Хёфдинга (вторая версия):
Пусть X1, X2, ..., Xn - независимые случайные величины, каждая из которых имеет значения в интервале [a, b]. Пусть S_n = (X1 + X2 + ... + Xn) / n - относительная частота наступления события. Тогда для любых положительных чисел ε и t неравенство Хёфдинга имеет следующий вид:
P(|S_n - E(S_n)| >= ε) <= 2e^(-2nt^2 / (b-a)^2).
Неравенство Бернштейна:
Для независимых случайных величин X1, X2, ..., Xn с ограниченными значениями и E(Xi) = μ для всех i, неравенство Бернштейна имеет вид:
P(|(1/n) * Σ(Xi) - μ| >= t) <= 2 * exp(-nt^2 / (2σ^2 + 2Mt/3)),
где σ^2 - дисперсия случайной величины Xi, M - максимальное абсолютное значение Xi - μ.
Это неравенство также позволяет оценить вероятность отклонения относительной частоты наступления события от его вероятности на основе ограничений на значения и дисперсию случайных величин.
Эти формулы позволяют оценить вероятность того, что отклонение относительной частоты наступления события от его вероятности не превысит заданную величину ε. Выбор конкретной формулы и её вариации зависит от характеристик случайных величин и требуемой точности оценки вероятности.