Предмет: Алгебра,
автор: Xonda7777
Найти производные n порядка.
Приложения:
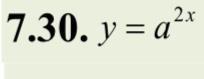
Ответы
Автор ответа:
2
Ответ:
Объяснение:
7x8:
:d
o_0
Похожие вопросы
Предмет: История,
автор: Zhanetochka
Предмет: Математика,
автор: zeropiyou
Предмет: История,
автор: Mumuky
Предмет: Математика,
автор: 999ship