Question

Помогите СРОЧНО 5 триугольниклв плачу 100 балов Сделайте и напишите как вы это делали

Answer 1

Объяснение:

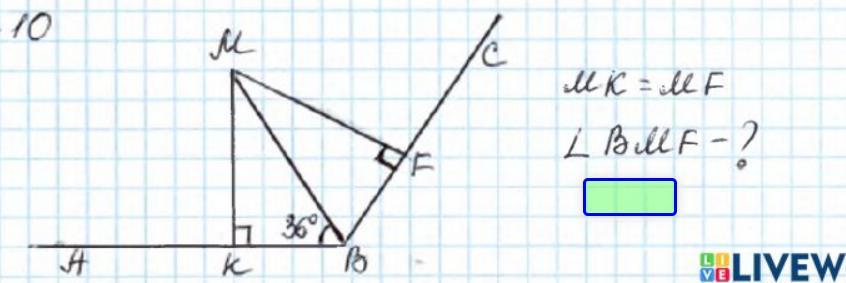
№10)

∆МКВ- прямоугольный треугольник.

Сумма острых углов в прямоугольном треугольнике равна 90°.

∠КМВ=90°-∠МВК=90°-36°=54°

∆МКВ=∆МВF, по пятому признаку равенства прямоугольных треугольников. (МВ- общая гипотенуза; МК=МF, по условию)

В равных треугольниках соответственные углы равны.

∠КМВ=∠ВМF=54°

Ответ: ∠ВМF=54°

_________________

№6)

∆APN- прямоугольный треугольник.

∠АNP=90°;

∠NAP=30°;

Катет NP против угла 30°;

NP=AP/2=10/2=5 ед

∆MNP- прямоугольный, равнобедренный треугольник.

∠РNM=90°; ∠NMP=45°; ∠MPN=45°. Углы при основании равны.

NP=NM=5 ед

Ответ: NM=5

_________________

№7)

∆ВКB- прямоугольный треугольник.

Сумма острых углов равна 90°

∠К=90°-∠NBK=90°-15°=75°

∆ABK- равнобедренный треугольник

АВ=АК, по условию. Углы при основании равны.

∠АВК=∠К=75°

∠АВN=∠ABK-∠NBK=75°-15°=60°

∆ABN- прямоугольный треугольник

∠ВNA=90°; ∠ABN=60°; ∠BAN=90°-∠ABN=90°-60°=30°

BN- катет против угла 30°

АВ=2*ВN=2*9=18 ед.

Ответ: АВ=18

____________________

№8)

∆AKP- прямоугольный треугольник

∠АКР=90°; ∠АРК=30°; ∠КАР=60°

АR- биссектриса.

∠RAP=30°; ∠RAK=30°;

∆АКR- прямоугольный треугольник

КR- катет против угла 30°;

АR=2*KR;

∆ARP- равнобедренный треугольник, углы при основании равны по 30°; АR=RP.

KR=x; AR=RP=2x.

KP=KR+RP=x+2x=3x; KP=18см

3х=18

х=6 см КR;

RP=2x=2*6=12см

RP=AR=12см

Ответ: АR=12см

____________________

№9)

∠МВС=∠МВА=30°, ВМ- биссектриса

МС- катет против угла 30°

ВМ=2*МС;

АМ=ВМ (обьяснение также как в номере 8)

МС=5; ВМ=10

Ответ: ВМ=10