Предмет: Математика,
автор: adekvat24na7
Решите неравенство пожалуйста 35 балов
Приложения:
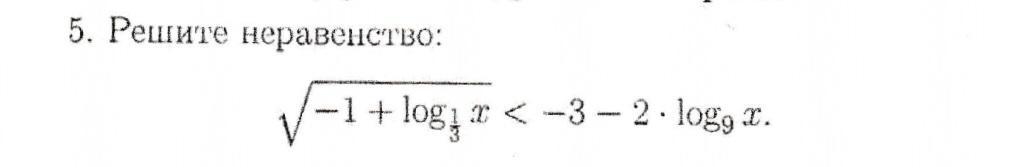
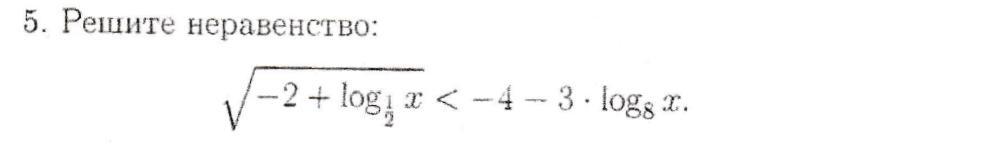
polarkat:
Так они одинаковые...
Ответы
Автор ответа:
1
-----------------------------------------------------
Приложения:
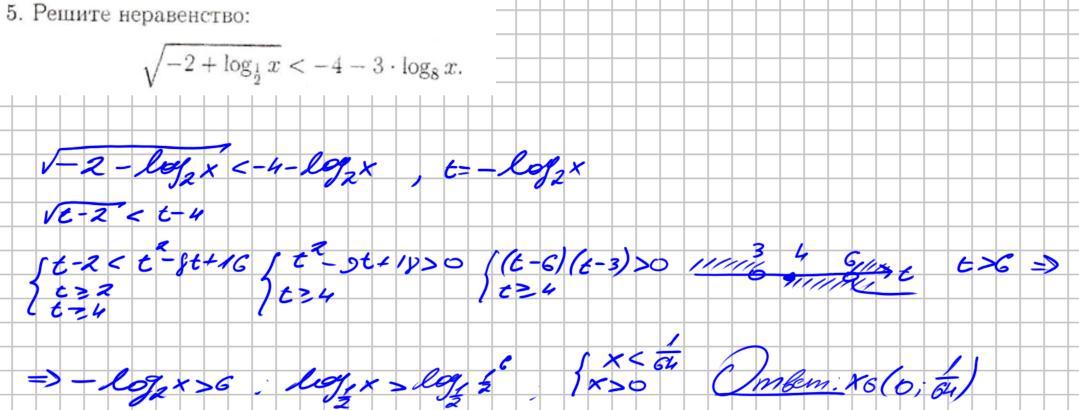

Автор ответа:
0
Ограничения и ответ
Второе неравенство такое же только с другими числами
Ограничения и ответ
Похожие вопросы
Предмет: Английский язык,
автор: nikitakalyuzhnyi08
Предмет: Химия,
автор: sherbananastasia1508
Предмет: Химия,
автор: omarrazab01
Предмет: Химия,
автор: sweetpea97
Предмет: Математика,
автор: ruzickchudakov