Предмет: Математика,
автор: adekvat24na7
Решите уравнение пожалуйста 25 баллов
Приложения:
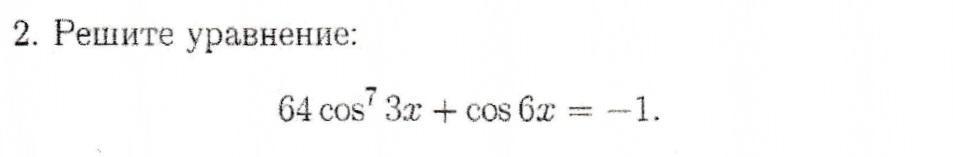
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Решите уравнение
По формуле половинного угла
Следовательно
Похожие вопросы
Предмет: Химия,
автор: sherbananastasia1508
Предмет: Химия,
автор: omarrazab01
Предмет: Физика,
автор: abuashvilimari
Предмет: Математика,
автор: ruzickchudakov
Предмет: Алгебра,
автор: almondi2010