Предмет: Математика,
автор: yopa12
Пусть n — целое положительное число. В Королевстве Селлке Аравия насчитывается 2018n+1 городов. Король Марк хочет построить дороги с двусторонним движением, соединяющие определенные пары городов, так что для каждого города C и целого числа  существует ровно n городов, которые находятся на расстоянии i от C. (Расстояние между двумя городами – это наименьшее количество дорог на любом пути между двумя городами.) Для каких n Марк может добиться этого?
существует ровно n городов, которые находятся на расстоянии i от C. (Расстояние между двумя городами – это наименьшее количество дорог на любом пути между двумя городами.) Для каких n Марк может добиться этого?
Ответы
Автор ответа:
0
Рассмотрим граф с городами в качестве вершин и дорогами в качестве ребер. Тогда каждая вершина имеет степень
, поэтому
Поскольку всегда четная, то
должно быть четным.
Теперь приведем конструкцию для четных . Для удобства пусть
и
. Пометим вершины
и соединим
и
, если
Этот граф полностью симметричен, поэтому достаточно показать, что это свойство выполняется для вершины . Разобьем остальные вершины на множества
Тогда , и именно вершины в
и
находятся на расстоянии
от
. Условие выполняется для вершины
, а значит, и для всех вершин
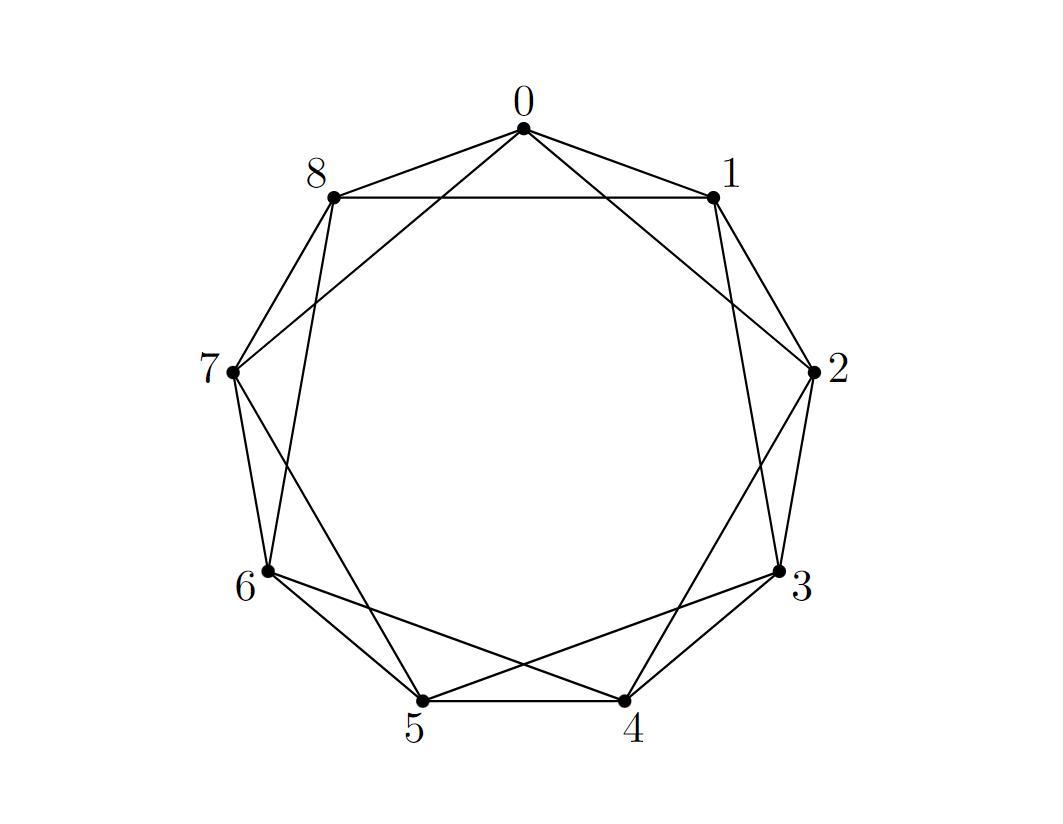
Приведем пример, в котором заменено на
и
. В этом случае имеем
,
,
,
. Тогда вершины в
и
находятся на расстоянии
, а вершины в
и
- на расстоянии
Приложения:
Похожие вопросы
Предмет: Українська література,
автор: akseniyashum
Предмет: Українська література,
автор: nikitanikit988
Предмет: Алгебра,
автор: lapt5058
Предмет: Математика,
автор: Nastia0096