Question

Докажите, что два круга на евклидовой плоскости радиусом меньше 1 не могут покрывать единичный круг

Answer 1

Довольно старая задача

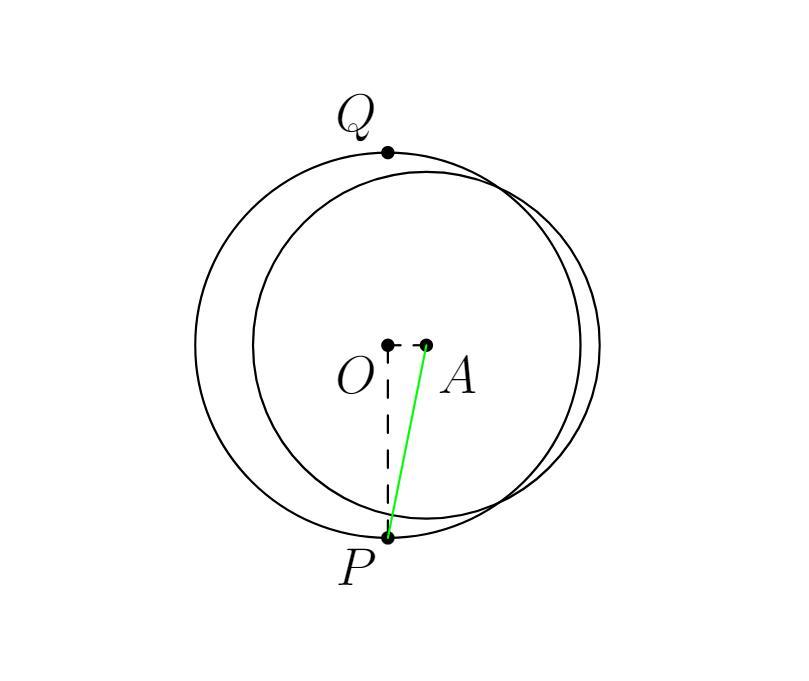
Пусть $O$ — центр единичного круга, а $A,B$ — центры двух других кругов. Пусть $P,Q$ — две точки на границе единичного круга с $\angle POA=\angle AOQ=90^\circ$. Тогда $AP^2=OP^2+OA^2\geq OP^2=1$, значит, $P$ лежит вне окружности с центром в $A$. Точно так же $Q$ лежит вне этого круга. Следовательно, чтобы покрыть весь единичный круг, круг с центром в $B$ должен содержать как $P$, так и $Q$. Но это невозможно, так как их расстояние равно $2$, что больше диаметра этой окружности