Question

Два кути паралелограма відносяться, як 1 : 3. Знайдіть кут між висотами паралелограма, проведеними з вершини: 1) тупого кута; 2) гострого кута.​

Answer 1

Відповідь:

1)Нехай  α - гострий кут параллелограма. Тоді кут  між висотами параллелограма, проведеного з гострого кута, дорівнює 180° - α.

Т.к. кути відносяться як  1:3, а їх сума дорівнює 180°, то складаємо  рівнення:

1х+3х=180

4х=180

х=45

знаходимо  гострий кут α = 1*45 =45

тоді , 180° - 45° = 135° кут між висотами паралелограма, проведеними з вершини: гострого кута.​

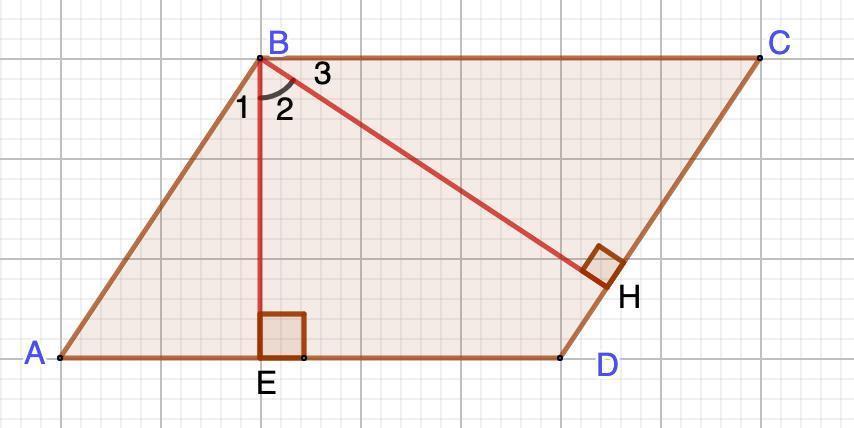
2)Дано: ABCD - параллелограмм.

∠А:∠В= 1:3

ВЕ и ВН - висоти

Знайти: ∠2

Рішення::

1. Знайдемо кути паралелограма

Кути паралелограма, що прилягають до однієї сторони, у сумі рівні 180°.

Нехай  ∠А=1х, тоді ∠В=3х.

Складаємо рівнення:

1х+3х=180°

4х=180°

х=45°

⇒ ∠А=1х=45°; ∠В=3х=135°

Протилежні кути  паралелограма рівні.

∠А=∠С=45°

∠В=∠D=135°

2. Разглянемо ΔАВЕ - прямокутний.

Сума гострих кутів  прямокутного трикутника= 90°.

⇒ ∠1=90°-∠А=90°-45°=45°

3. Разглянемо ΔВСН - прямокутний.

∠3=90°-∠С=90°-45°=45°

4. ∠2=∠В-(∠1+∠3)=135°-(45°+45°)=45°

Відповідь: кут між висотами паралелограма, проведеними з вершини: тупого кута дорівнює 45°

 

Пояснення:

фото- кут між висотами паралелограма, проведеними з вершини: тупого кута дорівнює 45°