Предмет: Математика,
автор: marl1nkes
У рінобедреному трикутнику бічна сторона=20, а основа=5, знайдіть бісектрису проведену з кута при основі до сторони!
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
ΔАВС: АВ=ВС=20, АС=5.
Биссектриса АК проведена из вершины А на ВС.
ВК+СК=ВС
ВК=20-СК
По свойству биссектрисы
АС/СК=АВ/ВК
5/СК=20/(20-СК)
100-5СК=20СК
СК=4
Тк. АВ=АС/2cos A
cos A=АС/2АВ=5/2*20=1/8
Углы при основании равны, значит cos A=cos С=1/8
По теореме косинусов:
АК²=АС²+СК²-2АС*СК*cos C=5²+4²-2*5*4*1/8=41-5=36
АК=6
Автор ответа:
0
Ответ:
6 см.
Пошаговое объяснение:
Бісектриса трикутника ділить протилежну сторону на відрізки, пропорційні двом іншим сторонам.
ВК/АК=ВС/АС
Нехай ВК=х, тоді АК=20-х см.
х/(20-х) = 20/5; х/(20-х)=4; х=4(20-х); х=80-4х; 5х=80; х=16.
ВК=16 см, АК=20-16=4 см.
АВ=ВС=АС/2cosA; cosA=AC/2AB=5:2*20=5/40=1/8
За теоремою косинусів
СК²=АС²+АК²-2*АС*АК*cosA=25+16-2*5*4*1/8=41-5=36; СК=√36=6 см.
Приложения:
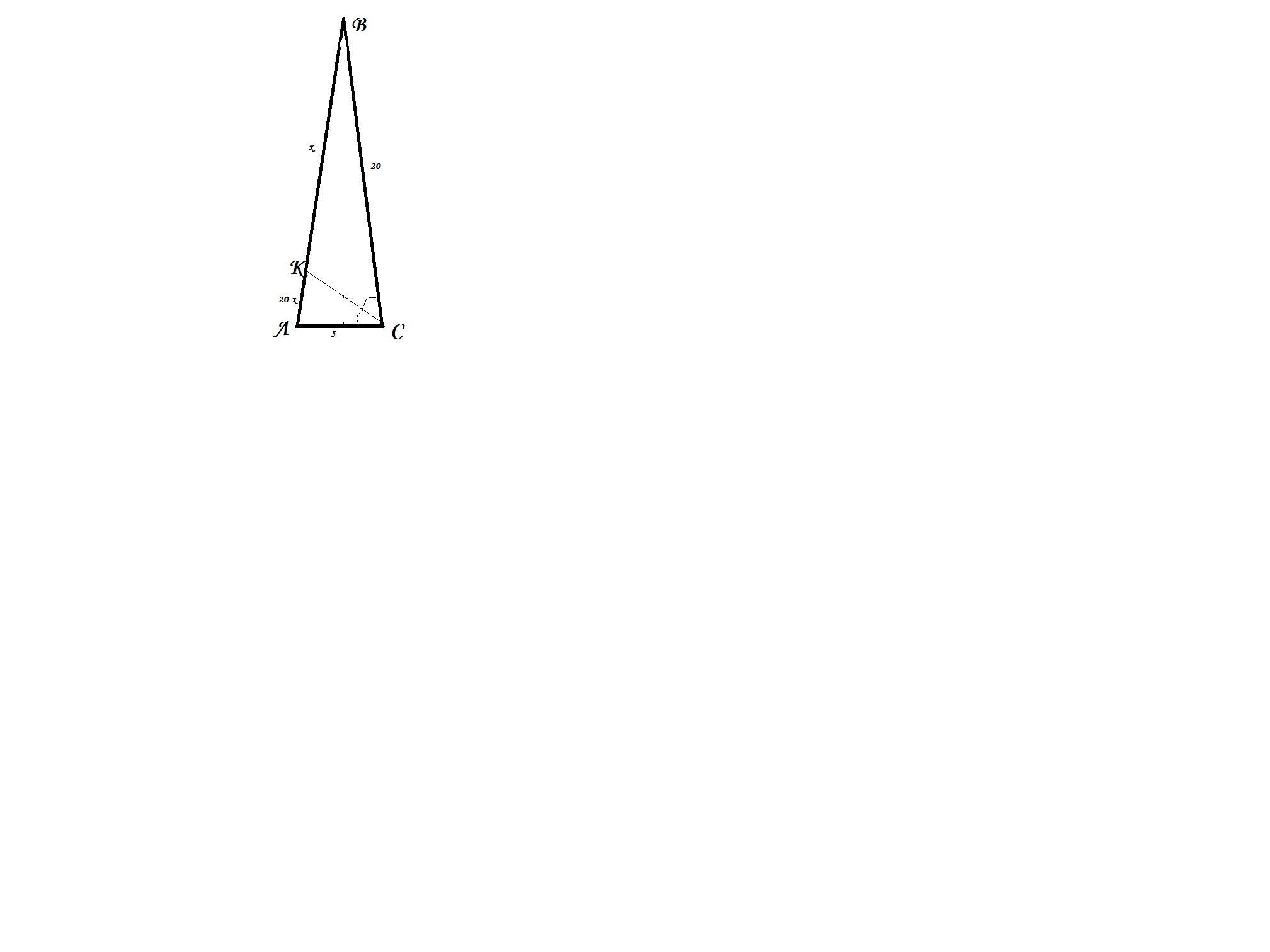
Похожие вопросы
Предмет: Алгебра,
автор: kirillryabchenko2007
Предмет: Математика,
автор: abbasovaaylin666
Предмет: Алгебра,
автор: kirillryabchenko2007
Предмет: Физика,
автор: raulimmedov
Предмет: Геометрия,
автор: Аноним