Предмет: Математика,
автор: ragimamamedova2008
Пожалуйста помогите
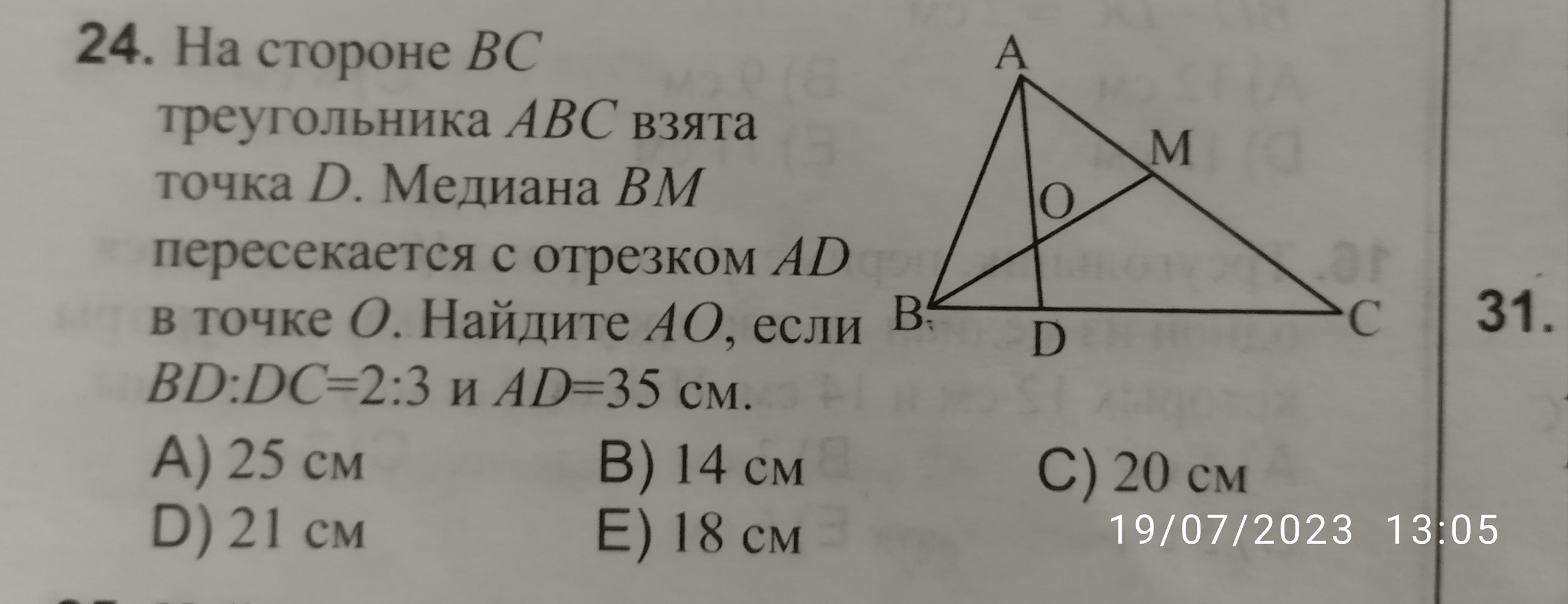
Условие на рисунке
Приложения:
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Воспользуемся теоремой Менелая. Прямая BM пересекает сторону AD треугольника ADC в точке O, сторону AC в точке M, продолжение стороны DC в точке B. Поэтому
Итак, в AO 5 частей, в OD 2 части. Поэтому AD делим на 5+2=7 частей (в одной части будет 35/7=5 см), длина AO равна 5·5=25 см.
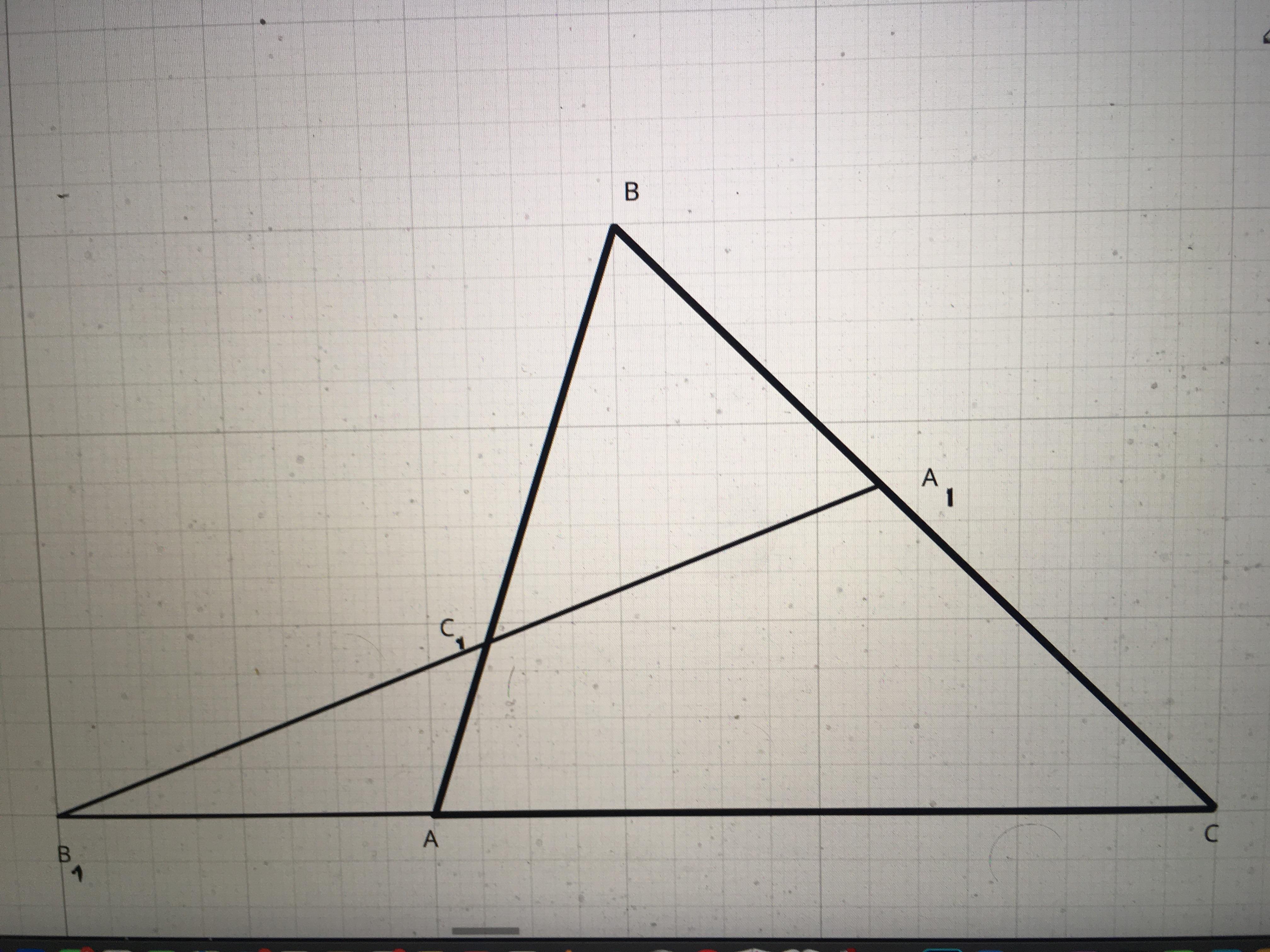
Теорема Менелая. Если прямая пересекает стороны AB, BC и CA треугольника ABC соответственно в точках (см. чертеж), то
Приложения:
ragimamamedova2008:
Спасибочки
Автор ответа:
1
Ответ:
25..........................
Пошаговое объяснение:
Приложения:

Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: nikaPopadiuk
Предмет: История,
автор: olgaevcuk28
Предмет: Геометрия,
автор: kriliusmudriy1234
Предмет: Геометрия,
автор: kriliusmudriy1234