Доведіть ознаку рівності трикутників за 2 сторонами й медіаною,проведенню до однієї з них
Ответы
Відповідь:
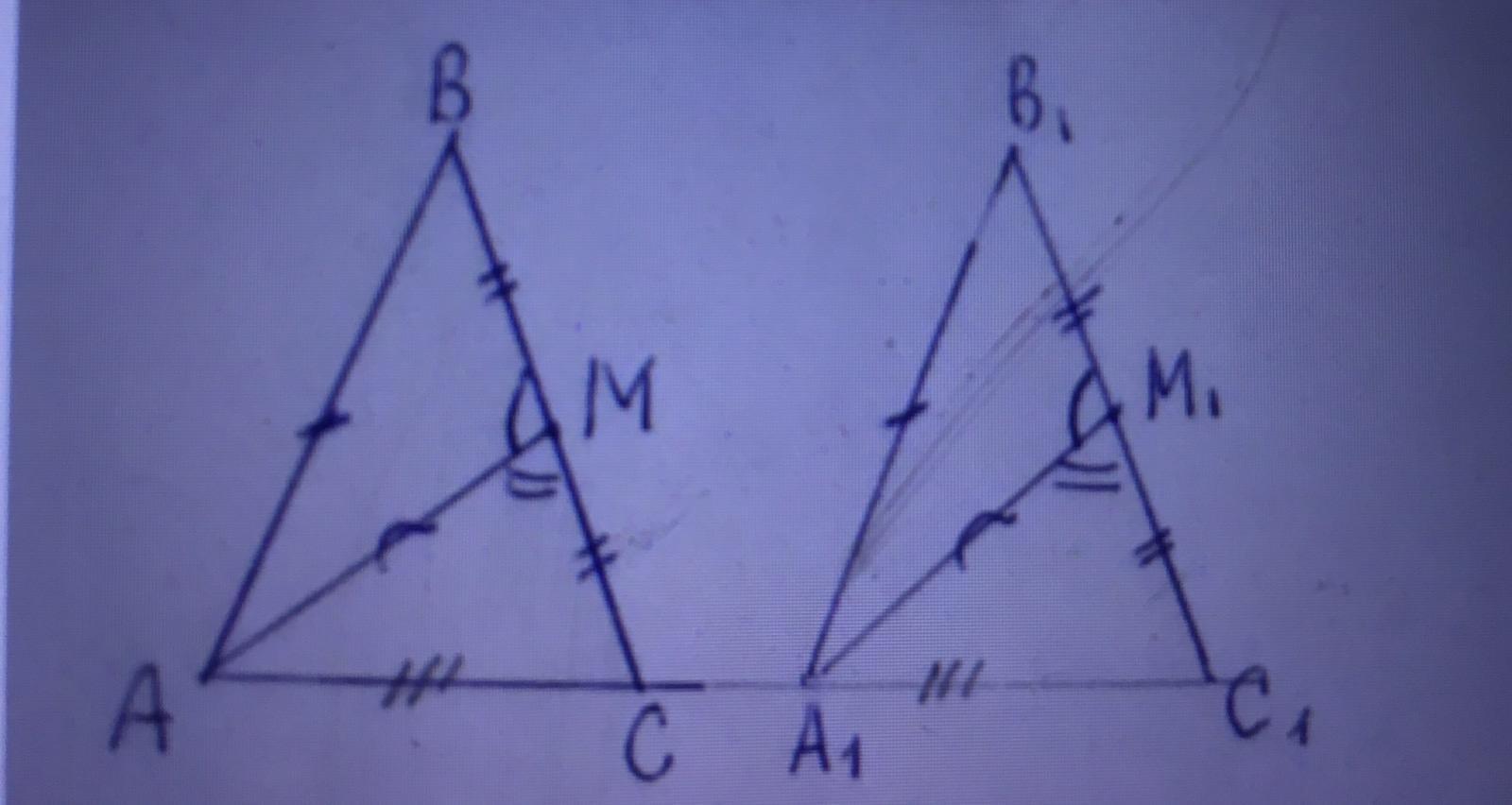
Розглянему трикутники АВС та А1В1С1
бічні сторони :АВ=ВС=А1В1=В1С1-за умовою
медіани: АМ=А1М1-за умовою
Доведіть ознаку рівності трикутників за 2 сторонами й медіаною,проведенню до однієї з них.
Рішення:
Розглянемо трикутники АВМ та А1В1М1
Медіани проведені до бічних сторін ВС та В1С1,тому поділяють ці сторони на дві рівні половини,тоді ВМ=МС= В1М1=М1С1.
Бічні сторони :АВ=ВС=А1В1=В1С1-за умовою,тому трикутники рівнобідрені.
ΔАВМ=ΔА1В1М1 - за трьома сторонами згідно третій ознаки рівності трикутників.(якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.)
∠АМС =∠А1М1С1=180-∠АМВ;
Розглянемо ΔАМС иΔА1М1С1
кути рівні за другим признаком рівності трикутників(кути рівні за другим признаком рівності трикутників):
АМ=А1М1-за умовою; МС=М1С1 та ∠АМС =∠А1М1С1
тоді АС=А1С1 ,отримуємо що ΔАВС = ΔА1В1С1 згідно третій ознаки рівності трикутників.(якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.)
АВ=ВС=А1В1=В1С1,та АС=А1С1,що і потрібно було доказати
Пояснення:
Відповідь:
Пояснення:
Можна довести рівність ΔАВС = ΔА₁В₁С₁ просто .
За умовою АВ = А₁В₁ і ВС = В₁С₁ . Якщо АМ і А₁М₁ - медіани даних
трикутників і АМ = А₁М₁ , то ВМ = МС = В₁М₁ = М₁С₁ ( за означенням
медіани тр - ника ) . За ІІІ - ю ознакою рівності тр - ників маємо
ΔАВМ = ΔА₁В₁М₁ . Звідси ∠В = ∠В₁ і , врахувавши , що АВ = А₁В₁ і
ВС = В₁С₁ , за І - ою ознакою рівності тр - ників ΔАВС = ΔА₁В₁С₁ .
Доведено ( досить просто ) .