Предмет: Математика,
автор: vladborisov177
В прямоугольном треугольнике АВС гипотенуза АВ равна 3, угол А равен а. Треугольник АВС вращается вокруг катета ВС. Найдите объем полученного тела вращения
Ответы
Автор ответа:
1
Ответ:
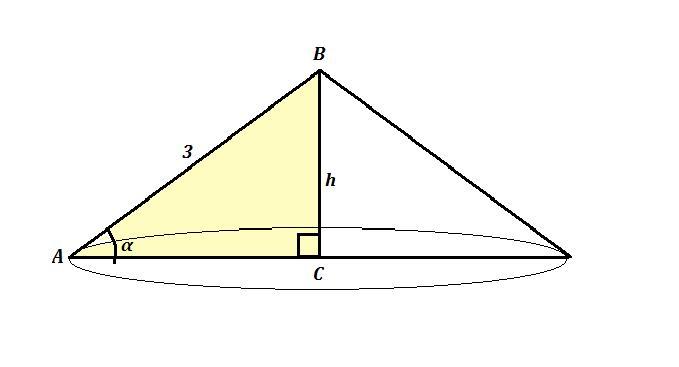
ΔАВС , ∠С=90° , ∠А = α , АВ = 3 .
Треугольник АВС вращается вокруг катета ВС. Найдите объем полученного тела вращения .
Тело вращения - это конус с высотой , равной h=ВС и образующей, равной АВ .
Объём конуса .
Из ΔАВС имеем :
Приложения:
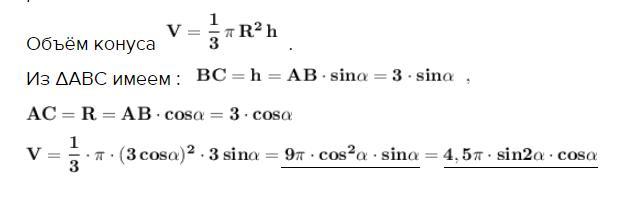
Похожие вопросы
Предмет: Химия,
автор: Hdjfkd
Предмет: Математика,
автор: vasilevaanna062004
Предмет: Английский язык,
автор: annasahakyan20202020
Предмет: Математика,
автор: egoregribov
Предмет: Математика,
автор: Radaev0303