Квадратная сетка на евклидовой плоскости состоит из всех точек (m,n), где m и n - целые числа. Можно ли покрыть все точки сетки бесконечным семейством дисков с непересекающимися внутренностями, если каждый диск семейства имеет радиус не менее 5?
Ответы
Идея и почему мы решили действовать так
На первый взгляд проблема кажется очень неприступной. Чтобы показать, что точка решетки существует, достаточно показать, что существует квадрат размером . Геометрия квадрата не очень хорошо сочетается со всеми кругами, поэтому вместо этого я попытался показать, что круг радиусом
существует. Число 5 можно получить, если взять и выложенные плиткой окружности так, чтобы центры образовывали равносторонние треугольники; быстрый расчет подтверждает, что 5 - это минимально необходимое число
Моя первоначальная идея состояла в том, чтобы соединить центры всех дисков и получить "паутину'", а затем показать, что в этой паутине существует треугольник, для которого при вырезании трех секторов в оставшейся области образуется искомый круг. Эта идея работает только в том случае, если в области любого треугольника паутины есть только три сектора, а не любые другие круги; но это неверно, если три круга расположены очень далеко друг от друга и в область входит четвертый круг
Чтобы модифицировать эту идею, я рассматривал расширение окружности до тех пор, пока она не попадет на некоторые три диска, вместо того чтобы фиксировать их
Решение
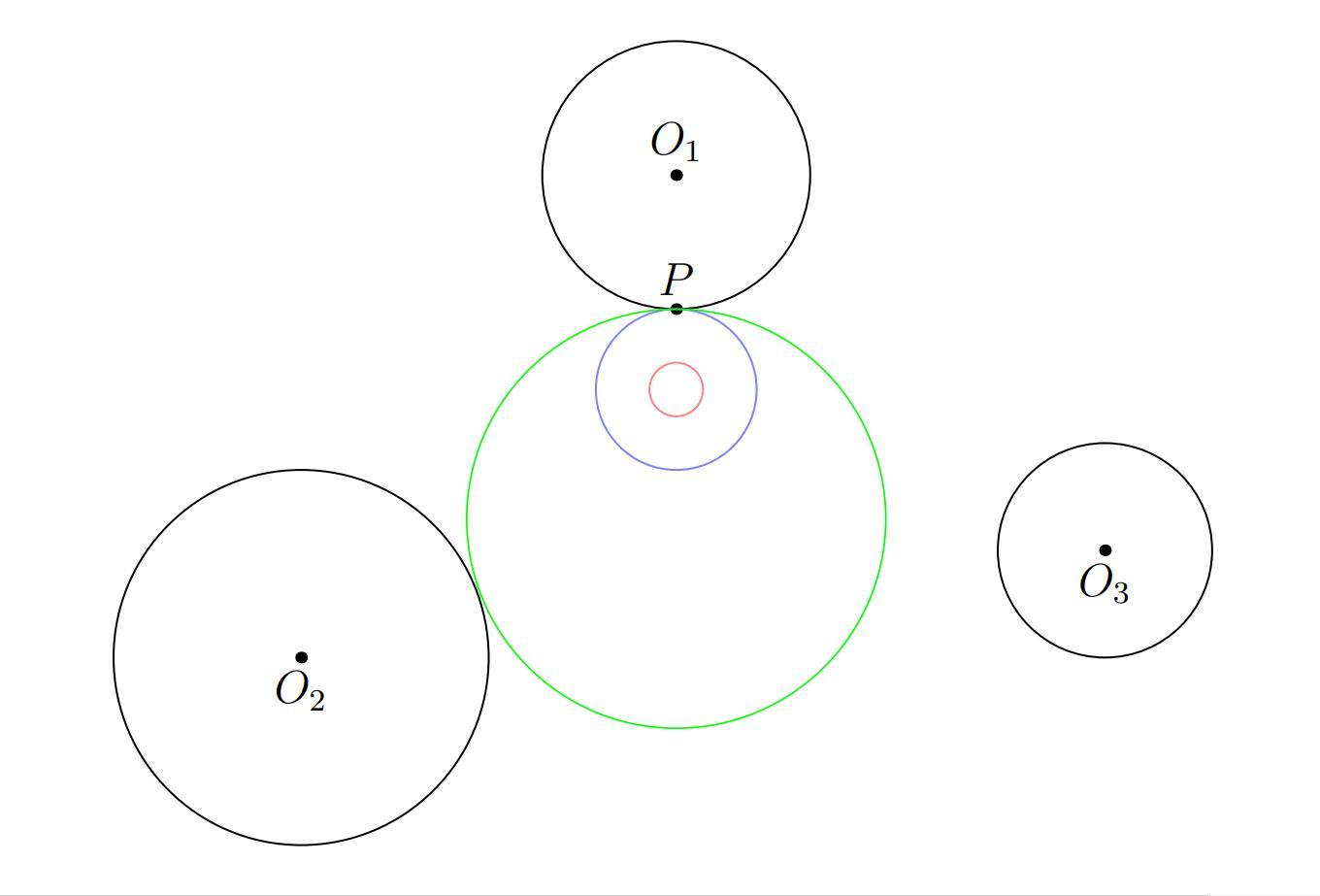
Предположим, что это возможно. Основная идея состоит в том, чтобы показать, что можно получить окружность радиусом не менее , не пересекающую ни один диск; тогда эта окружность должна содержать квадрат
, в котором находится точка решетки. Начнём с точки
и красной окружности с центром в
, которая не пересекает никакую окружность
- Возьмем гомотетию в точке
, пока новая окружность (закрасьте ее синим цветом) не станет касательной к некоторому диску
в точке
- Возьмем гомотетию в точке
, пока новая окружность (закрасьте ее зеленым цветом) также не станет касательной к некоторому диску
- Расширяем зеленую окружность, сохраняя ее касательной к
и
, пока она не станет касательной к диску
Лемма: Конечная окружность имеет радиус не менее
Доказательство: В каждой вершине существует окружность в точке
радиуса
. Если эти три окружности не попарно касательны, то можно немного увеличить один из радиусов, что уменьшит радиус
Поэтому предположим, что окружности
попарно касательны.
, тогда в треугольнике
мы получаем
P.S.
Рисунок рисовал в , возможно криво получилось