Предмет: Алгебра,
автор: Iklg
Знайти область визначення і значень
Приложения:

polarkat:
Найти нужно только область определения и значения функции и всё?
Да
И задание 2;3
Ответы
Автор ответа:
3
Ответ:
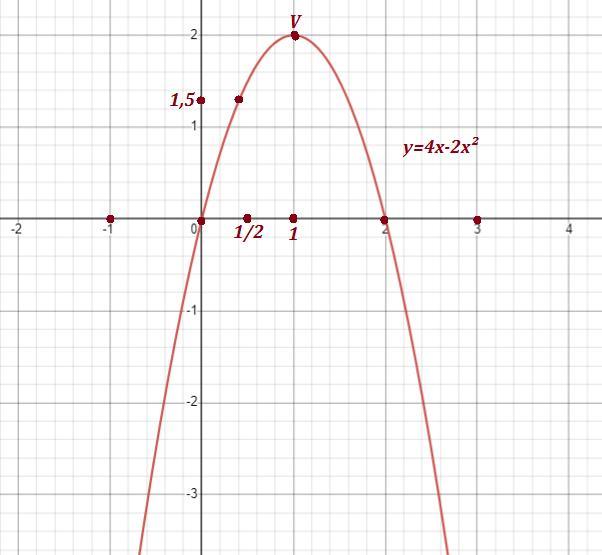
Построить график функции .
Нули функции :
Вершина параболы :
- вершина параболы .
Не существует точек, в которых функция принимает значение, равное 3 , так как область изменения функции - это промежуток (-∞ ; 2 ] .
3) Наибольшее значение функции : .
Приложения:


Похожие вопросы
Предмет: Алгебра,
автор: voznuk037
Предмет: Алгебра,
автор: gdhtecbjjyj
Предмет: История,
автор: ynka1612
Предмет: Алгебра,
автор: remoulded
Предмет: Математика,
автор: dannil567