Предмет: Алгебра,
автор: a9799027
Решите неравенство, пожалуйста
Приложения:
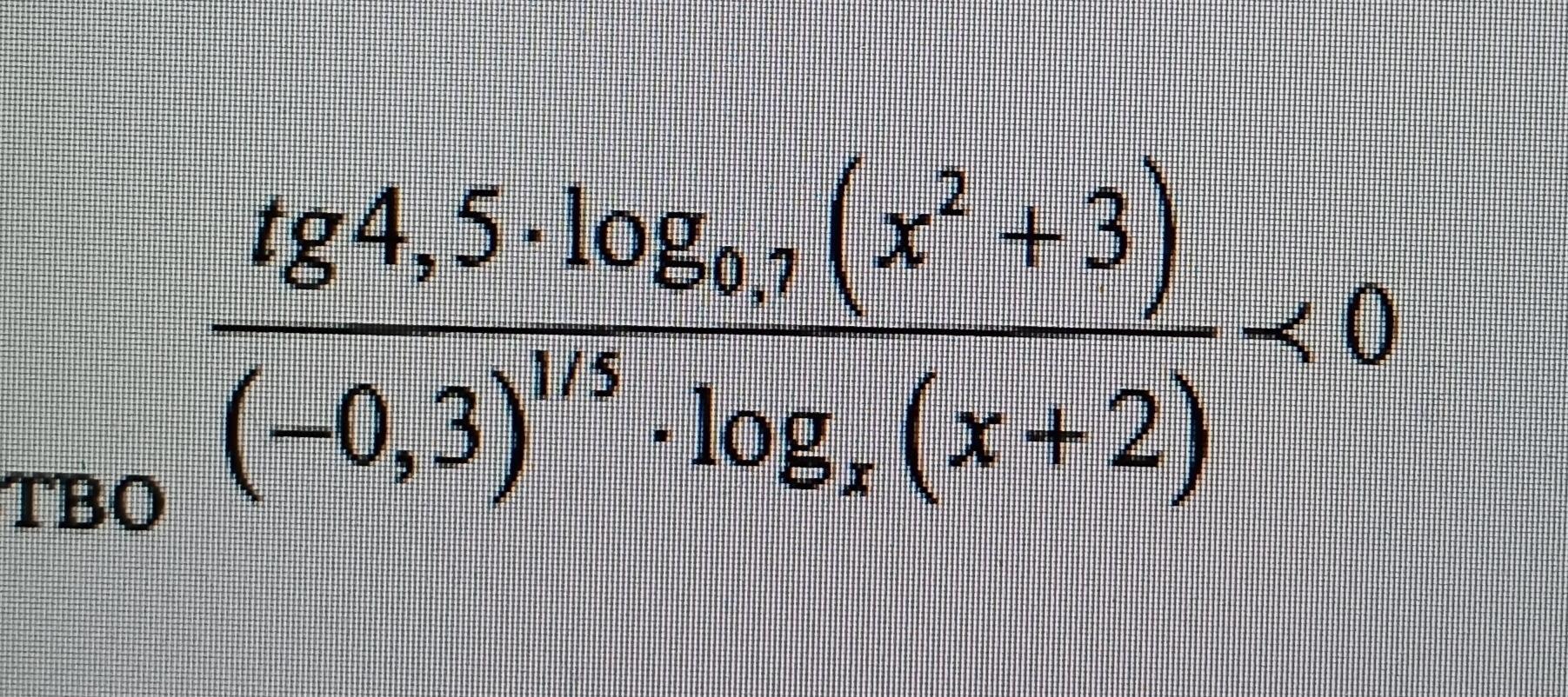
Inte1gral:
Теперь уже настоящее задание?) (o・ω・o)
Да)
Вроде бы (0; 1), ответы пока заняты умными людьми
Ответы
Автор ответа:
1
В знаменателе перед логарифмом отрицательное число, а в числители положительное, давайте домножим на них, чтобы избавится, но при делении или умножении на отрицательное число, знак неравенства нужно поменять
Так же стоит заметить, что числитель не имеет нулей, да и сама функция всегда будет ниже нуля из-за своего основания, значит, мы может поделить на числитель, но не забыть, поменять знак, так как функция принимает только отрицательные значения
Теперь нам нужно найти все ограничения и нанести их на наш ответ
С учётом наших ограничений, решением будет
Похожие вопросы
Предмет: Химия,
автор: lera96354
Предмет: Українська мова,
автор: x4533337
Предмет: Английский язык,
автор: leyla2880
Предмет: Математика,
автор: milana54678
Предмет: Английский язык,
автор: feedfoxis