Предмет: Алгебра,
автор: RuLam
решите то что на фото
Приложения:
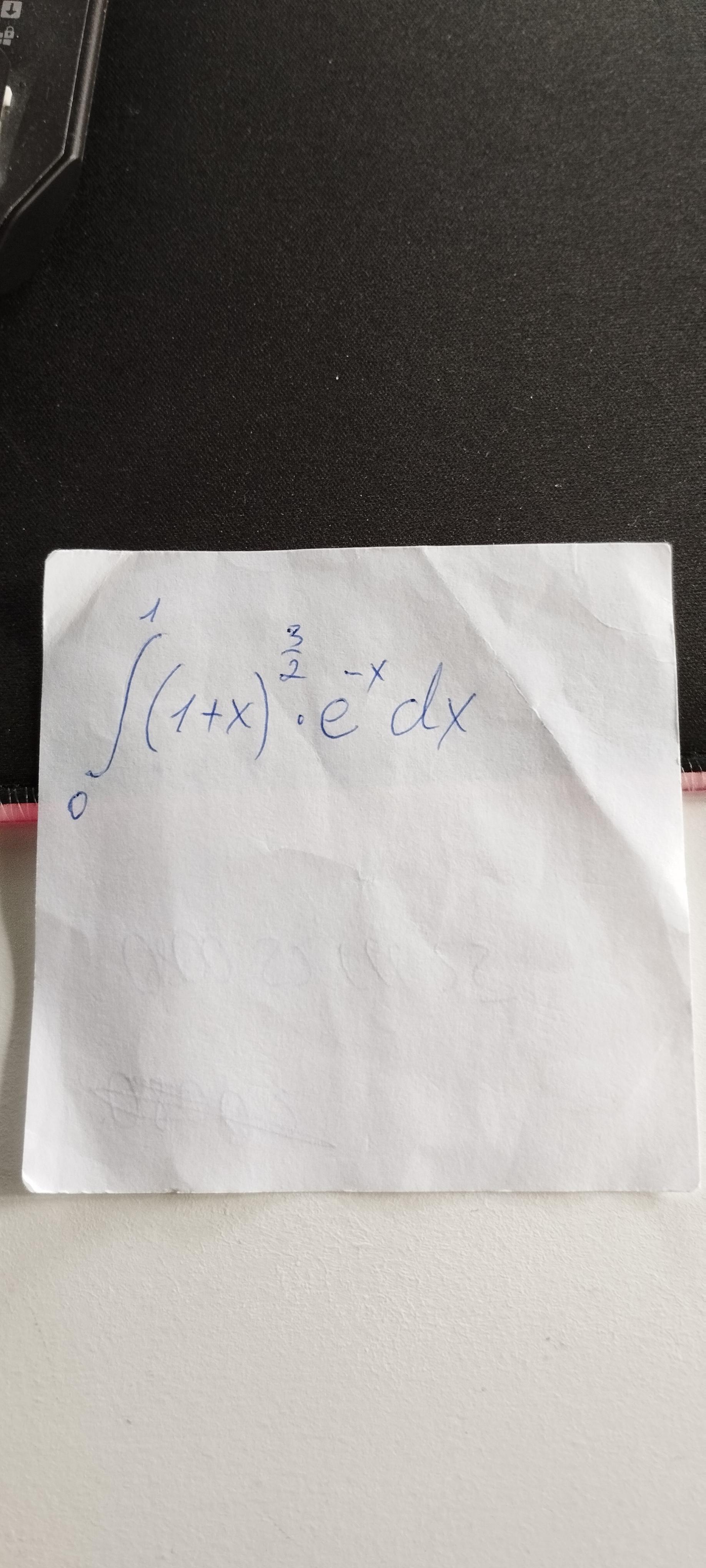
Ответы
Автор ответа:
1
Сначала вычислим неопределённый интеграл, сделав подстановку
Интегрируем по частям
тогда получаем
Но это в чистом виде определение функций ошибок Гаусса, то есть
А значит
где можно функцию ошибок Гаусса выразить через гамма-функцию, то есть
Похожие вопросы
Предмет: Английский язык,
автор: eresenkoveronika
Предмет: Литература,
автор: yaneznaunichego
Предмет: Английский язык,
автор: eresenkoveronika
Предмет: Математика,
автор: sjdosbdkd
Предмет: Математика,
автор: milana54678