Предмет: Геометрия,
автор: matvaliyevasay81
В правильной четырехугольной пирамиде боковое ребро равно 6√2, а угол между ним и плоскостью основания равен 45°. Найдите объем пирамиды.
Здравствуйте) не могу понять помогите пожалуйста
Ответы
Автор ответа:
0
Ответ: 144 см³.
Объяснение:
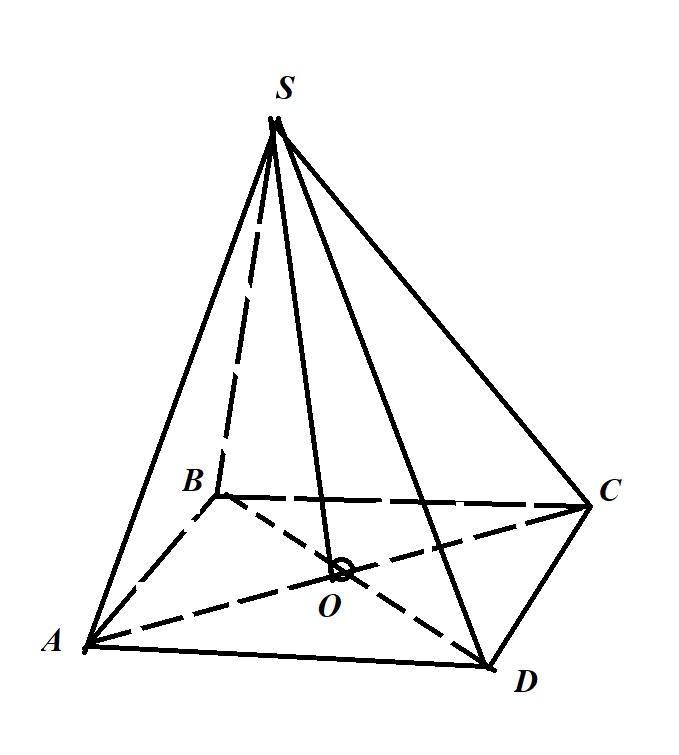
SABCD - четырехугольная пирамида
V(SABCD)=1/3* S осн*H. H-высота пирамиды.
S осн.=AB*BC = 6√2*6√2 = 36*2 = 72 см².
H²=SC² -OC²; OC = AC/2; AC-диагональ основания
AC²=AB²+BC² = (6√2)²+(6√2)² = 72+72 = 144;
AC=12 см
OC = 1/2AC = 12/2 = 6 см.
Н²=(6√2)² - 6² = 72-36 = 36;
H=√36 = 6 см.
S(SABCD) = 1/3*S осн*H = 1/3*72*6 = 144 см³.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: bezmudko
Предмет: Информатика,
автор: alphagenerationkidsc
Предмет: Русский язык,
автор: ksamzyy
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: ustinovat17