Предмет: Геометрия,
автор: ogabektoshpulatov108
От точки, расположенную на расстоянии 6 см от центра круга, проведены две касательные. Расстояние между точек касания равен 3 см. Найдите радиус круга??
ppp6491:
У меня радиус круга получился 1,5529... см. Такой ответ имеется?
Ответы
Автор ответа:
2
Ответ:
Объяснение:
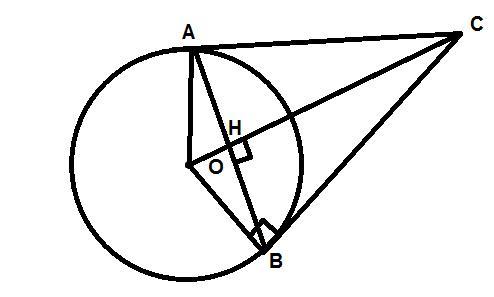
Пусть две касательные были проведены с точки C, точки касания A и В, окружность с центром О, тогда АВ=3, ОС=6.
1) OACB-дельтоид, следоватльно угол между диагоналями прямой, а точка их пересечения(пусть Н) будет делить одну из диагоналей пополам(в данном случае AH=HB=1,5)
2) угол ОBC-прямой(радиус к касательной). Если угол OCB обозначить за 90-α, угол СОВ=α, а радиус за r, то можно составить такую систему(равенства взяты из треугольников ОСВ и ОНВ, углы острые) :
Приложения:
Не люблю к
к-тригонометрия?
"кривых" ответов! И часть Вашего ответа не видна!!!
Телефон " шалит".
ааа. Та вроде должна быть видна, в самом верху
Ну да. Ответ виден.
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Английский язык,
автор: tina1801
Предмет: Українська мова,
автор: anastasiapobeda80
Предмет: Физика,
автор: aleksejcertolas444