Предмет: Математика,
автор: rudskojfejs
Знайти площу рівнобедренного трикутника, якщо його бічна сторона дорівнює 6 см., а кут при основі 60°.
Бажано з розв'язком.
Ответы
Автор ответа:
1
Если угол при основании равен 60, то треугольник равносторонний
Приложения:
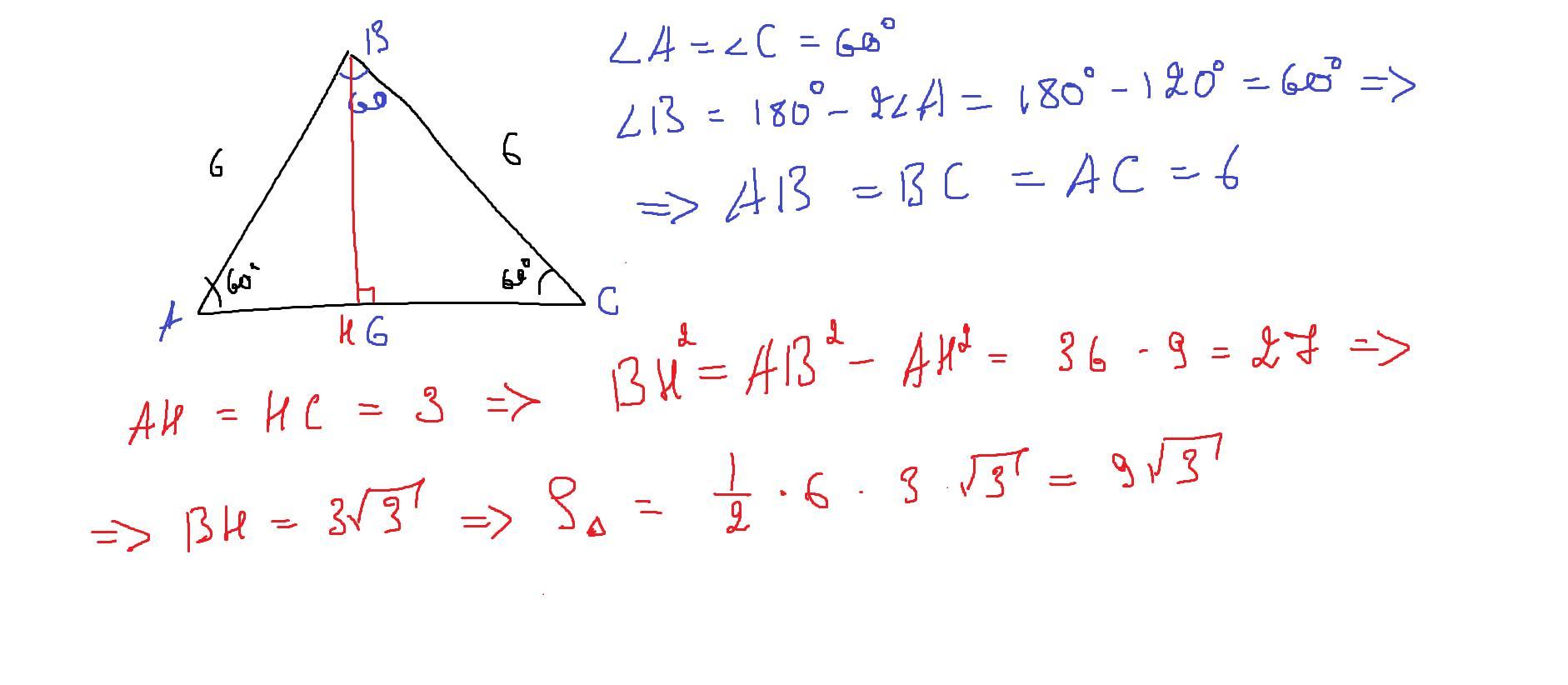
Автор ответа:
0
Ответ:
9√3 см².
Пошаговое объяснение:
1. Пусть ∆ АВС равнобедренный с основанием АС.
По условию ∠ВАС = 60°, тогда и ∠ВСА = ∠ВАС = 60° (углы при основании равнобедренного треугольника). По теореме о сумме углов треугольника третий угол ∠АВС = 180° - (60° + 60°) = 60°.
Все углы треугольника равны, тогда равны и все его стороны, ∆АВС равносторонний.
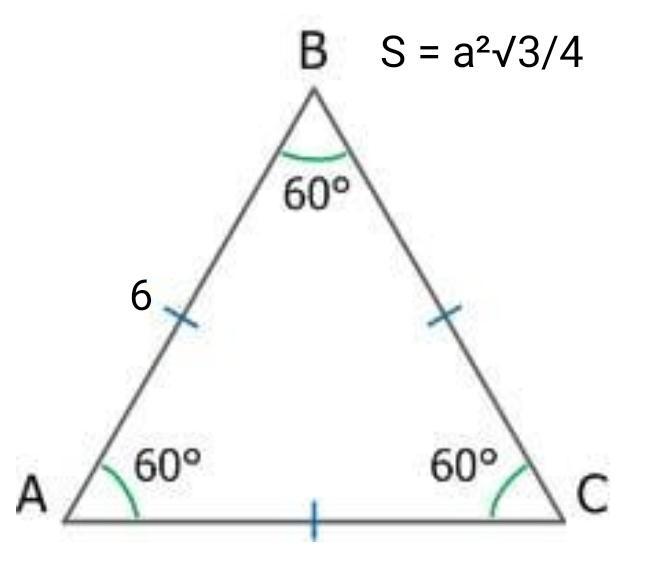
2. Площадь равностороннего треугольника со стороной а по теореме можно найти по формуле
S = a²•√3/4.
В нашем случае
S = 6²√3/4 = 9√3 (см²).
Приложения:
Похожие вопросы
Предмет: История,
автор: dashamal08
Предмет: Математика,
автор: dilya031052
Предмет: Литература,
автор: skaspryshyn
Предмет: Английский язык,
автор: plov234
Предмет: Литература,
автор: sofiyaSkladovskaya