Question

Решите задачу подробно с рисунком. текст задачи во вложении.​

Answer 1

Ответ: 60 градусов.

Объяснение:

решение о вложении.

Answer 2

Решение.

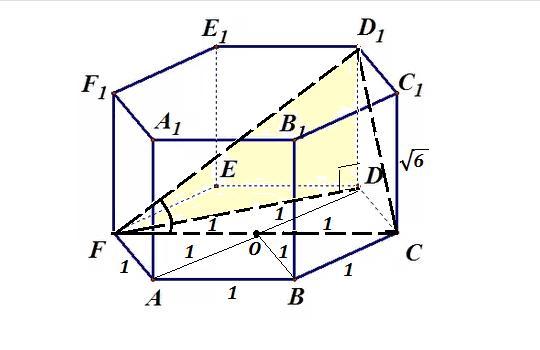
Дана правильная шестиугольнfя призма ABCDEFA₁B₁C₁D₁E₁F₁  .

Значит в основании лежит правильный шестиугольник ABCDEF .

Правильный шестиугольник делится своими диагоналями на 6 равных равносторонних треугольника : ΔАОВ=ΔВОС=ΔCOD=ΔDOE=ΔEOF=ΔAOF .  

Стороны этих треугольников равны радиусу описанной окружности R :  AB=BC=CD=DE=EF=FA=R=1    ⇒  

FC = OF+OC = 1+1 = 2 - это диаметр описанной окружности .

Боковое ребро равно  √6 .  

Чтобы найти угол между АВ и FD₁  , надо найти отрезок, параллельный АВ , и найти угол между ним и FD₁  .

FC || АВ   ⇒   искомый угол - это ∠CFD₁  .  

FC = 2R = 2·1 = 2

Найдём  СD₁  по теореме Пифагора из прямоугольного  ΔСDD₁ :  

CD₁² = CD²+CD₁² = 1+(√6)²=1+6=7  ,   CD₁ = √7  

Рассмотрим ΔEFD , ∠DEF=120°  как внутренний угол правильного шестиугольника .  Известно по условию, что EF = ED = 1 . Найдём по теореме косинусов сторону FD .

FD² = EF²+ED²-2·EF·ED·cos∠DEF = 1+1-2·1·1·cos120° = 2 - 2·(-1/2) = 2+1 = 3

FD = √3

Рассмотрим ΔDFD₁ ,  ∠D₁DF=90° .  Найдём  FD₁  по теореме Пифагора :   FD₁² = FD² + DD₁² = 3 + 6 = 9  ,   FD₁ = √9 = 3  

Рассмотрим  ΔCFD₁  . Применим теорему косинусов :

CD₁² = FC²+FD₁² - 2 · FC · FD₁· cos∠CFD₁  

7 = 2² + 9 - 2 · 2 · 3 · cos∠CFD₁  

7 = 13 - 12 · cos∠CFD₁  

12 · cos∠CFD₁ = 13 - 7  

cos∠CFD₁ = 6/12  ,   cos∠CFD₁ = 1/2   ⇒     ∠CFD₁ = 60°        

Угол между  АВ  и  FD₁  равен  60°  .