Question

помогите пожалуйста! задание закреплено в фотографии​

Answer 1

Ответ:

Расстояние от точки О до точка А равно 4√5 ед.

Объяснение:

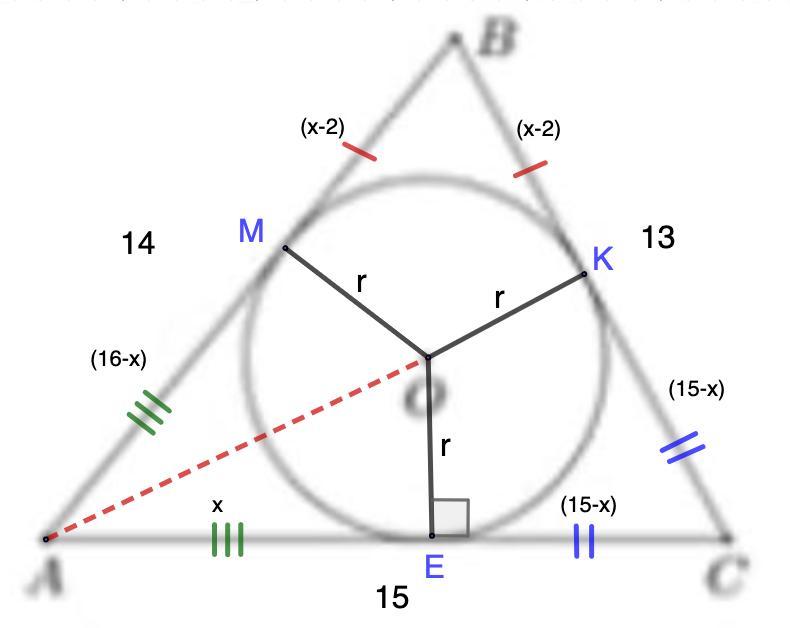
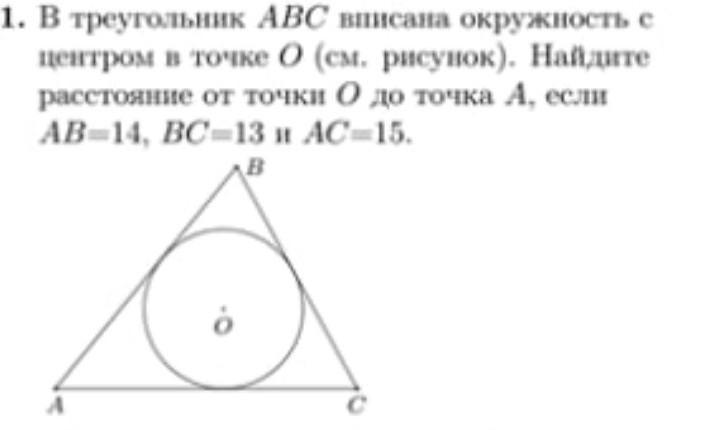
В треугольник АВС вписана окружность с центром в точке 0 (см. рисунок). Найдите расстояние от точки О до точка А, если АВ=14, ВС=13 и АС=15.

Дано: ΔАВС;

АВ-14, ВС=13 и АС=15.

Окр.(О; r) - вписана в ΔАВС

Найти: ОА

Решение:

Проведем радиусы ОЕ, ОМ, ОК.

• Радиус вписанной окружности найдем по формуле:

                          $\displaystyle \bf r=\frac{2S}{a+b+c}$,

где S - площадь треугольника, a, b, c - его стороны.

• Площадь треугольника найдем по формуле Герона:

                       $\displaystyle \bf S=\sqrt{p(p-a)(p-b)(p-c)}$,

где р - полупериметр треугольника.

р = (14 + 13 + 15) : 2 = 21

$\displaystyle S=\sqrt{21\cdot(21-14)(21-13)(21-15)}=\\ \\=\sqrt{7\cdot3\cdot7\cdot4\cdot2\cdot2\cdot3}=7\cdot3\cdot2\cdot2=84$

Можем найти r:

$\displaystyle r=\frac{2\cdot84}{14+13+15} =4$

ОЕ = 4

• Отрезки касательных, проведенных из одной точки, равны.

Пусть АЕ = х, тогда ЕС = 15 - х;

ЕС = КС = 15 - х, тогда ВК = 13 - (15 - х) = х - 2;

ВК = ВМ = х - 2, тогда АМ = 14 - (х - 2) = 16 - х

АМ = АЕ  ⇒   16 - х = х

2х = 16     |:2

x = 16

AE = 16

Рассмотрим ΔАОЕ.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ΔАОЕ - прямоугольный.

• По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.

⇒ ОА² = ОЕ² + АЕ² = 16 + 64 = 80   ⇒   ОА = √80 = 4√5

Расстояние от точки О до точка А равно 4√5 ед.