Предмет: Математика,
автор: yatsenko8838
Нужно решить 1 пример по математике
Приложения:

Ответы
Автор ответа:
0
Решение .
Решить дифференциальное уравнение . Уравнение с разделяющимися переменными .
Ответ представить в виде .
Приложения:
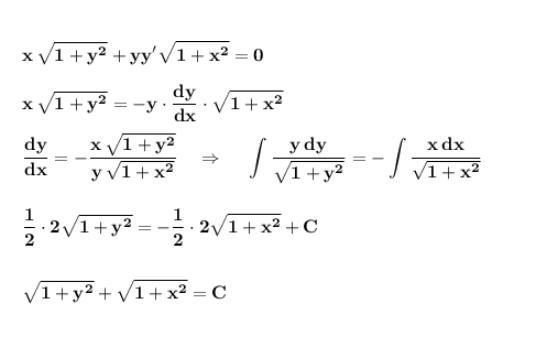
Похожие вопросы
Предмет: Математика,
автор: ruslanaesekeeva180
Предмет: Английский язык,
автор: Аноним
Предмет: Другие предметы,
автор: sofijakruglova18
Предмет: Английский язык,
автор: Alexander2232