Предмет: Алгебра,
автор: mitzuki058
Доказать ограниченность последовательности:

antonovm:
она по модулю меньше 1 , возведите её модуль в квадрат и докажите , что он меньше 1 для всех n , а значит и сам модуль меньше 1 , что и означает её ограниченность . Студенты вам решат , если было непонятно
Ответы
Автор ответа:
1
Сначала рассмотрим производную от функции , то есть
Очевидно, что когда , то
, поэтому
убывает
Рассмотрим
А значит , следовательно,
ограничена
Автор ответа:
1
Ответ:
...................................................
Объяснение:
Приложения:
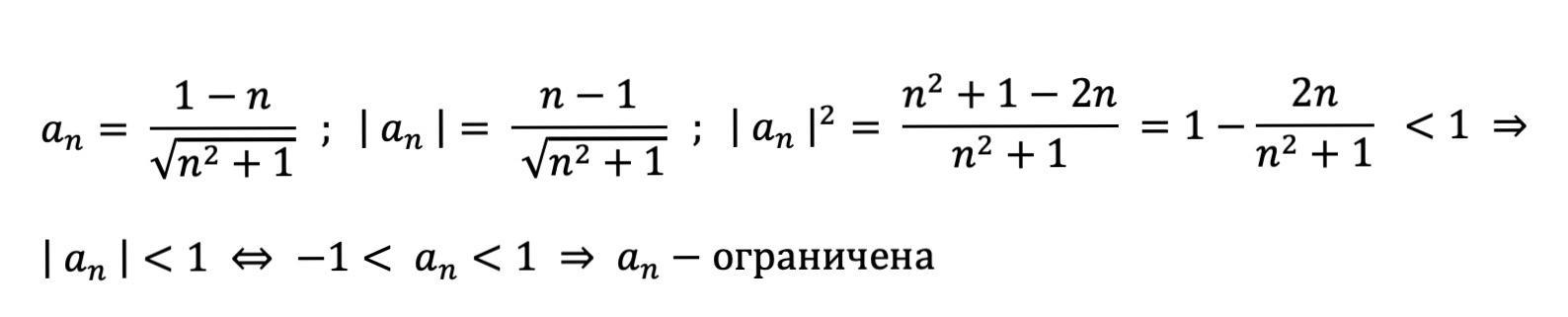
можете решить последний вопрос что я задала
Похожие вопросы
Предмет: Другие предметы,
автор: sofijakruglova18
Предмет: Алгебра,
автор: alinasenuchena74
Предмет: Математика,
автор: anastasiadorofii
Предмет: Русский язык,
автор: Аноним