Предмет: Математика,
автор: dariacas06
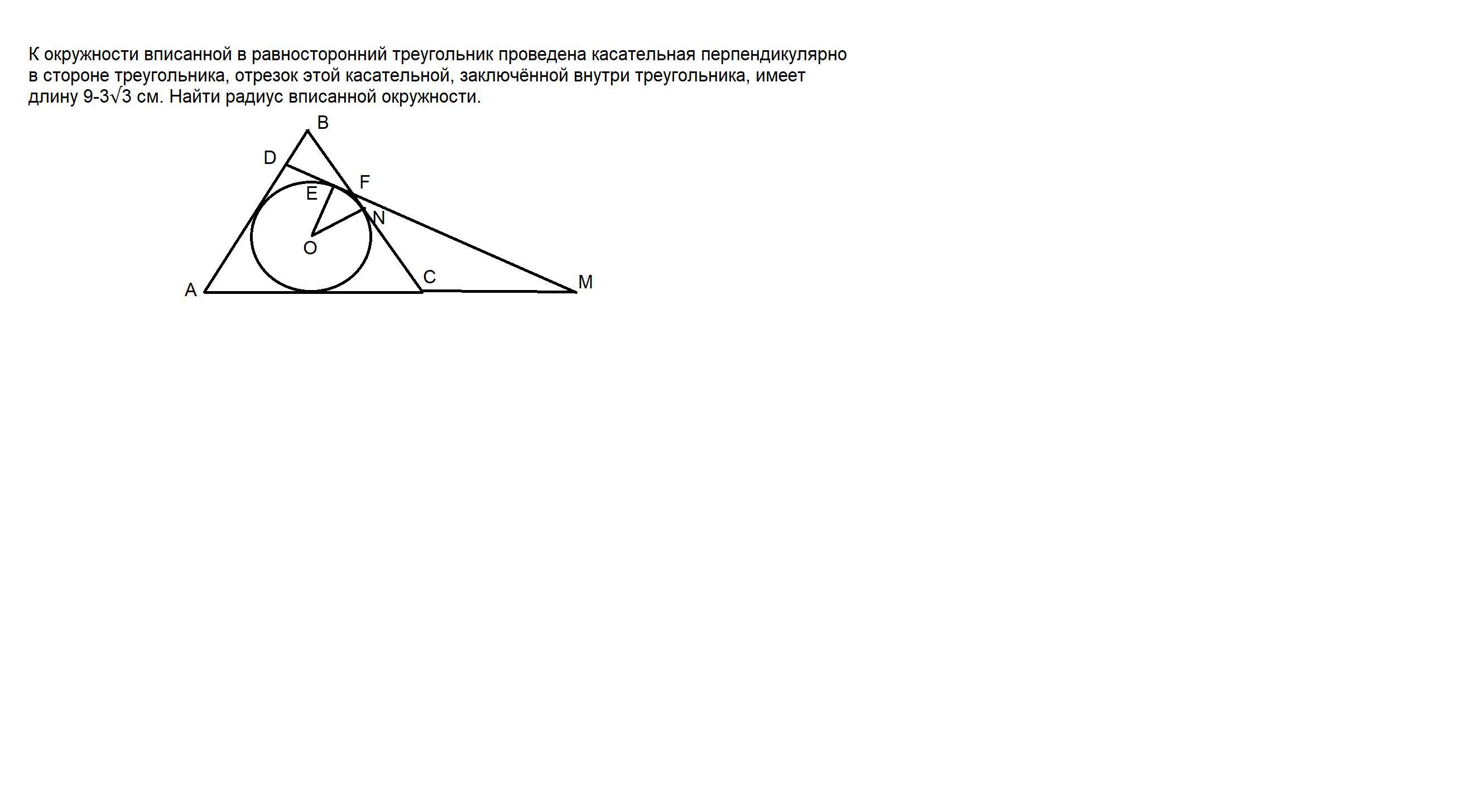
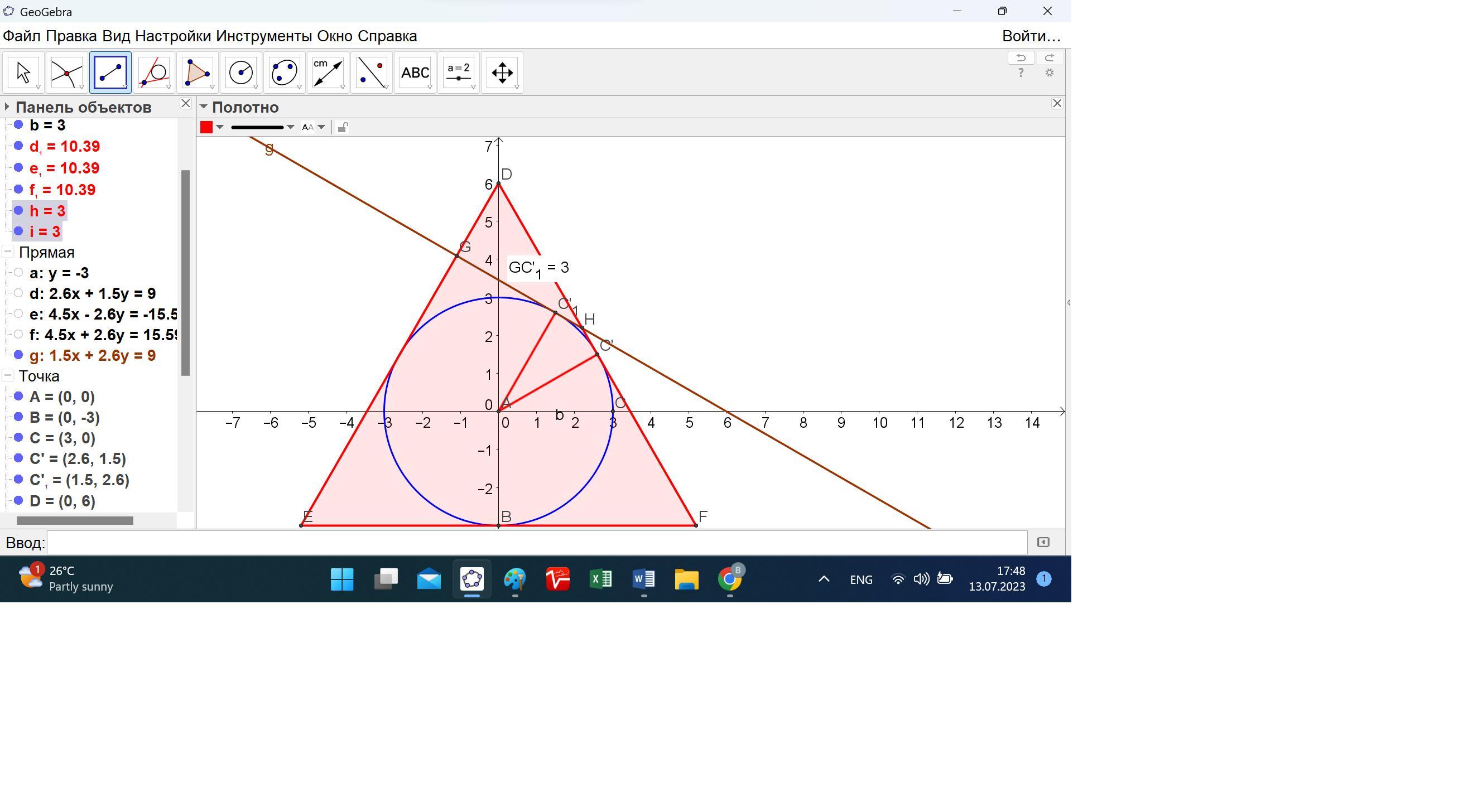
К окружности вписанной в равносторонний треугольник проведена касательная перпендикулярно в стороне треугольника, отрезок этой касательной, заключённой внутри треугольника, имеет длину 9-3√3 см. Найти радиус вписанной окружности.
Ответы
Автор ответа:
0
Ответ: 3 см.
Пошаговое объяснение:
Угол EON как взаимно перпендикулярный к касательным DM и BC равен 30 градусов.
ЕF = Rtg(30°/2) = R (1 – (√3/2))/(1/2) = 2R(1 – (√3/2)).
DE = R.
По заданию DF = 9 - 3√3.
Так как DF = DE + ЕF = R + 2R(1 – (√3/2)).
9 - 3√3 = = R + 2R(1 – (√3/2)).
Отсюда R = (9 - 3√3)/(1 + 2(1 – (√3/2)) = (9 - 3√3)/(1 + 2 – √3) = 3(3 - √3)/(3 - √3) = 3.
Приложения:
Автор ответа:
2
3 см
##################
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: lukyanova201207
Предмет: Литература,
автор: Dinsi2018
Предмет: Математика,
автор: sofijakruglova18
Предмет: Геометрия,
автор: tanyagolub1982
Предмет: Биология,
автор: borisovkirill012