Предмет: Геометрия,
автор: soficalovica908
як це робиться? якщо можна то поясніть будь ласка
Приложения:
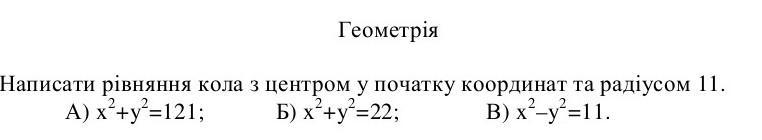
zmeura1204:
А) х²+у²=121
Ответы
Автор ответа:
1
Ответ:
Рiвняння кола з центром у початку координат та радiусом 11 мае вид:
Объяснение:
Напишемо рiвняння кола
(1)
де а - вiдстань вiд центра кола до початку координат по осi абсцисс
b - вiдстань вiд центра кола до початку координат по осi ординат
r - радiус кола
За умовою задачi центр кола знаходяться у початку координат. Тодi вiдстань вiд центра кола до початку координат по осi абсцисс дорiвнюе нулю, тобто a=0.
Вiдстань вiд центра кола до початку координат.по осi ординат дорiвнюе нулю, тобто b=0
Пiдставимо цi значення у рiвняння (1). Маемо:
Отже, рiвняння кола з центром у початку координат та радiусом 11 мае вид:
Вiдповiдь:
дякую))
Похожие вопросы
Предмет: География,
автор: kuzyapo
Предмет: Українська мова,
автор: klfax
Предмет: Українська мова,
автор: solomiiamerzliak
Предмет: Литература,
автор: terkina0081
Предмет: Математика,
автор: panpasha123